complexconjugate
- 3
- 0
- TL;DR
- How to calculate electromagnetic radiation contributions for a given observer
Hi!
I am dealing with the propagation of electromagnetic emissions through the atmosphere. To quickly outline:
Imagine some charge distribution flying at relativistic speeds and inducing a four-potential A. We define some retarded time at which the charges are at some positions, and calculate the observer time (the advanved time for the emission time) by integrating over the refractive index of the atmosphere. So far so good.
If you plot the retarded time t* over observer time t, you get these multi-branch functions, like in this plot:
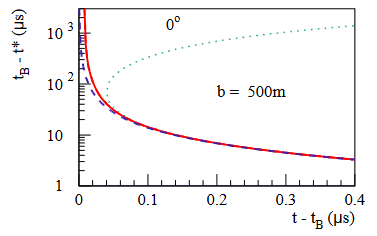
t is the observer time, t* is the emission time, t_B is just some plot relevant parameter. The different line styles correspond to different refractive indices (solid = realistic, dashed = 1, dotted = 1.0003).
If I want to calculate the contribution for an observer at time t, t* gives multiple possible solutions. If I want to go the other way and want to calculate where the emission for a given t* ends up, I feel like I can in essence just iterate over all my possible t* and tally up when in time it arrives.
As you can see in the plot, many retarded times are compressed into very short observer times and I am not sure how to deal with that properly. If I had infinite precision it would be fine, but my data will be binned in time, and (for the solid line) emissions from t* = 10³ to t* = 10² end up in the same t bin. Do I add all of these? That was my first instinct but then the bin values depend on my sampling rate of t*. Do I scale the contributions to each bin with dt*/dt or something similar? This feels both trivial and somehow just beyond my grasp...
Further, does someone have experience with taming these multibranch functions? Again, would I just add the different t* contributions into their shared t bin?
I hope my question is clear (and belongs here), let me know if you need more info.
PS, I didn't want to open several threads in a short time, but if anyone has Jefimenko's equations for non-vacuum media or literature in that direction, I'd be very grateful.
Cheers!
I am dealing with the propagation of electromagnetic emissions through the atmosphere. To quickly outline:
Imagine some charge distribution flying at relativistic speeds and inducing a four-potential A. We define some retarded time at which the charges are at some positions, and calculate the observer time (the advanved time for the emission time) by integrating over the refractive index of the atmosphere. So far so good.
If you plot the retarded time t* over observer time t, you get these multi-branch functions, like in this plot:
t is the observer time, t* is the emission time, t_B is just some plot relevant parameter. The different line styles correspond to different refractive indices (solid = realistic, dashed = 1, dotted = 1.0003).
If I want to calculate the contribution for an observer at time t, t* gives multiple possible solutions. If I want to go the other way and want to calculate where the emission for a given t* ends up, I feel like I can in essence just iterate over all my possible t* and tally up when in time it arrives.
As you can see in the plot, many retarded times are compressed into very short observer times and I am not sure how to deal with that properly. If I had infinite precision it would be fine, but my data will be binned in time, and (for the solid line) emissions from t* = 10³ to t* = 10² end up in the same t bin. Do I add all of these? That was my first instinct but then the bin values depend on my sampling rate of t*. Do I scale the contributions to each bin with dt*/dt or something similar? This feels both trivial and somehow just beyond my grasp...
Further, does someone have experience with taming these multibranch functions? Again, would I just add the different t* contributions into their shared t bin?
I hope my question is clear (and belongs here), let me know if you need more info.
PS, I didn't want to open several threads in a short time, but if anyone has Jefimenko's equations for non-vacuum media or literature in that direction, I'd be very grateful.
Cheers!