- #1
zenterix
- 480
- 70
- TL;DR Summary
- The measurement of the heat capacity of solids is cited in the book I am reading as one of the most important experimental projects of physics at the beginning of the 20th century because numerical values of heat capacity provide a direct means of assessing validity of assumptions used in statistical mechanics. I'd like to understand the experiment.
Consider the problem of measuring the heat capacities of solids using an electrical method where a resistance wire is wound around a cylindrical sample of the material.
Why and how is the dissipated energy in the first case considered work and not simply an internal exchange of heat (which sums to zero)?
I'd like to understand the following explanation of modern calorimetry from the book I am reading
As you can see, there is no mention of ##n## in the text, and yet it appears in the equation for the molar heat capacity. I assume it is the number of moles, which would make sense since then we'd have energy over time divided by the number of moles.
One of my questions is about the comment that the graph is really of resistance of the resistance thermometer vs time.
As I understand it, a resistance thermometer is an apparatus for which we can measure changes in resistance as we vary conditions in which it is immersed. To each resistance we assign a temperature, given a specific reference point (triple point of water) that receives the temperature 273K.
A different thermometer could have been used, for example a constant volume gas thermometer (probably impractical for a solid though).
In any case, it is temperature that is measured, though there is also the underlying thermometric property that defines the temperature scale (resistance in the resistance thermometer, pressure in the constant volume gas thermometer).
Why did the author feel the need to point out that the relationship is between resistance and time and not temperature and time.
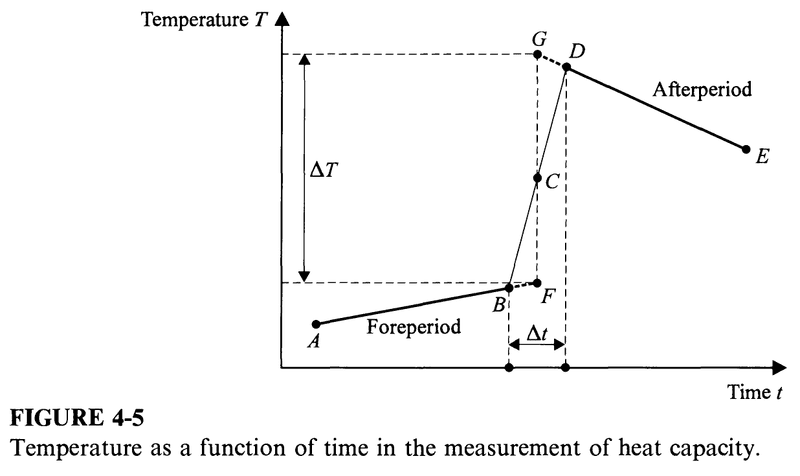
Furthermore, what is with the extrapolating of the foreperiod and afterperiod to reach G and F, and why is the molar heat capacity associated with point C and not point B?
If both the wire and the sample are regarded as the system, the the electrical energy dissipated in the wire is interpreted as work. When the wire is not included as part of the system, however, the energy which is dissipated within the wire and which flows into the sample by virtue of the temperature difference between the wire and sample (however small) is designated as heat.
Why and how is the dissipated energy in the first case considered work and not simply an internal exchange of heat (which sums to zero)?
I'd like to understand the following explanation of modern calorimetry from the book I am reading
In modern calorimetry, particularly in the case of solids at low temperatures, the sample is suspended in a highly evacuated space by means of fine threads of nylon or some other poorly conducting material. A heating coil is wound around the sample, and a thermocouple or a resistance thermometer (platinum, carbon, or germanium, depending on the temperature range) is placed in a small hole drilled for that purpose. The connecting wires for the heater, for the current in the thermometer, and for the potential difference across the thermometer are made very thin so as not to allow much heat to be transferred between the sample and its surroundings through the connecting wires.
The temperature of the sample is measured as a function of time; when plotted as in Fig. 4-5, this gives the line AB, marked "foreperiod". At the time corresponding to point B, a switch is closed and a current is established in the heater at the same moment that an electronic timer is started. After a short interval of time ##\Delta t##, the switch is opened and the timer is stopped. Then, the temperature is again measured as a function of time and is plotted as the line DE, marked "afterperiod" in Fig. 4-5.
As a rule, no reading of temperature or time is attempted while the timer is on, that is, from B to D. A vertical line is drawn through the center C of the line BD, and both the foreperiod and the afterperiod lines are extrapolated to this vertical line, giving the points F and G, as shown. The molar heat capacity ##C_P## at the temperature corresponding to point C is then given by
$$C_P=\frac{EI\Delta T}{n\Delta T}$$
where ##E## is the potential difference across the resistance wire and ##I## is the current in the wire.
Sometimes ##\Delta T## is made as small as 0.001 deg. Strictly speaking, the graph shown in Fig. 4-5 is not a graph of temperature ##T## vs. time ##t##, but of the resistance ##R'## of the resistance thermometer vs. time ##t##. Typically, the entire ##R'(t)## curve is digitized and the molar heat capacities are calculated by computer.
As you can see, there is no mention of ##n## in the text, and yet it appears in the equation for the molar heat capacity. I assume it is the number of moles, which would make sense since then we'd have energy over time divided by the number of moles.
One of my questions is about the comment that the graph is really of resistance of the resistance thermometer vs time.
As I understand it, a resistance thermometer is an apparatus for which we can measure changes in resistance as we vary conditions in which it is immersed. To each resistance we assign a temperature, given a specific reference point (triple point of water) that receives the temperature 273K.
A different thermometer could have been used, for example a constant volume gas thermometer (probably impractical for a solid though).
In any case, it is temperature that is measured, though there is also the underlying thermometric property that defines the temperature scale (resistance in the resistance thermometer, pressure in the constant volume gas thermometer).
Why did the author feel the need to point out that the relationship is between resistance and time and not temperature and time.
Furthermore, what is with the extrapolating of the foreperiod and afterperiod to reach G and F, and why is the molar heat capacity associated with point C and not point B?