- 15,882
- 9,050
I concur with @TSny. For future reference, when the sum of any number of vectors is zero and you add them using the graphical "tip-to-tail" graphical construction, you end with a closed polygon. The number of sides is equal to the number of forces that are added.
Here you have a right triangle because there are 3 forces and ##F_w## and ##F_g## are perpendicular (see below). All you have to do is figure out which of the interior acute angles should be labeled ##\alpha## and then write down the usual trig relations.
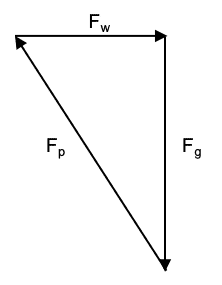
Here you have a right triangle because there are 3 forces and ##F_w## and ##F_g## are perpendicular (see below). All you have to do is figure out which of the interior acute angles should be labeled ##\alpha## and then write down the usual trig relations.