SUMMARY
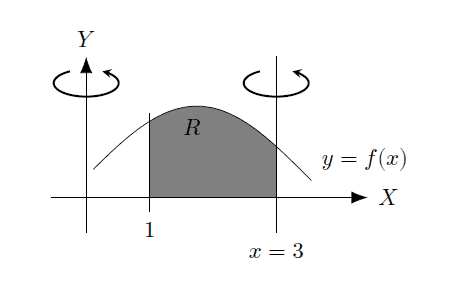
The volume of region R when revolving around the line x=3 using the shell method is calculated as Vx=3 = 2π ∫13 (3-x) f(x) dx. Given that the area of R is 2 m² and the volume when revolving around x=0 is 4π m³, the correct application of the shell method yields the desired volume. The user successfully derived the formula after multiple attempts, confirming the effectiveness of the shell method for this problem.
PREREQUISITES
- Understanding of the shell method in calculus
- Familiarity with definite integrals
- Knowledge of volume calculation for solids of revolution
- Basic proficiency in evaluating integrals involving functions
NEXT STEPS
- Study the shell method for different axes of rotation
- Learn how to derive volumes using the disk method
- Explore applications of definite integrals in real-world scenarios
- Practice problems involving the calculation of volumes of revolution
USEFUL FOR
Students studying calculus, educators teaching integration techniques, and anyone interested in mastering the shell method for calculating volumes of solids of revolution.