- #1
operationsres
- 103
- 0
ECONOMETRICS CALCULUS.
1. The PRECEDING question and solution
Differentiate
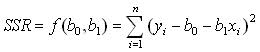 with respect to b1
with respect to b1
My solution:
df(b0,b1)/db1 = 2Σ[(yi-b0-b1xi)*(-xi)]
2. the ACTUAL question
By setting d,f(b0,b1)/d,b1 = 0, show that you obtain
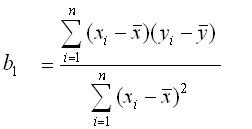 .
.
(Hint: you will have to substitute b0 = yBAR - b1(xBAR), and use the results from the previous question.)
3. Some properties that we can assume while answering the question.
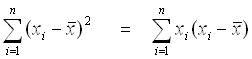
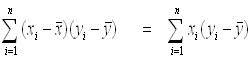
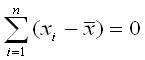
4. The attempt at a solution (I can't do it)
Letting 2Σ[(yi-b0-b1xi)*(-xi)] = 0
0= Σ[(yi-b0-b1xi)*(-xi)]
0= Σ(-yi xi)+Σb0xi+ Σb1xi ^2
0= -Σ (yi xi)+b0 Σxi+b1Σxi^2
b1Σxi^2=Σyi Σxi – (yBAR-b1xBAR)Σxi ... (Re-arranging and substituting for b0)
b1Σxi=Σyi -yBAR+b1xBAR ...... (dividing both sides by Σxi)
b1Σxi – b1xb = Σyi – yBAR
b1(Σxi – xb)=Σyi – yBAR
b1= (Σyi – yb)/(Σxi – xBAR)
= (Σyi – Σyi /n)(Σxi – Σxi/n)
1. The PRECEDING question and solution
Differentiate
My solution:
df(b0,b1)/db1 = 2Σ[(yi-b0-b1xi)*(-xi)]
2. the ACTUAL question
By setting d,f(b0,b1)/d,b1 = 0, show that you obtain
(Hint: you will have to substitute b0 = yBAR - b1(xBAR), and use the results from the previous question.)
3. Some properties that we can assume while answering the question.
4. The attempt at a solution (I can't do it)
Letting 2Σ[(yi-b0-b1xi)*(-xi)] = 0
0= Σ[(yi-b0-b1xi)*(-xi)]
0= Σ(-yi xi)+Σb0xi+ Σb1xi ^2
0= -Σ (yi xi)+b0 Σxi+b1Σxi^2
b1Σxi^2=Σyi Σxi – (yBAR-b1xBAR)Σxi ... (Re-arranging and substituting for b0)
b1Σxi=Σyi -yBAR+b1xBAR ...... (dividing both sides by Σxi)
b1Σxi – b1xb = Σyi – yBAR
b1(Σxi – xb)=Σyi – yBAR
b1= (Σyi – yb)/(Σxi – xBAR)
= (Σyi – Σyi /n)(Σxi – Σxi/n)
Last edited: