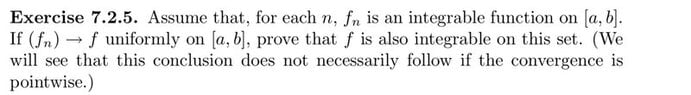Riemann integrability and uniform convergence

[lys04]

Was reading the Reimann integrals chapter of Understanding Analysis by Stephen Abbott and got stuck on exercise 7.2.5. In the solutions they went from having |f-f_n|<epsilon/3(a-b) to having |M_k-N_k|<epsilon/3(a-b), but I’m confused how did they do this. We know that fn uniformly converges to f, that means for any epsilon greater than 0 I can find natural number M st when n is greater than M then the distance from fn to f is less than epsilon for all x in the interval [a,b], but the supremums of fn and f in a sub interval [x_k-1,x_k] might occur at different values and I’m not sure how they’re meant to be at most epsilon apart.

 

[Office_Shredder]

I suspect it's a typo and the 3 in the denominator is supposed to be gone.

Edit: actually I take it back. Let's say $M_k>N_k$. Then where $M_k$ is realized, $f_N$ is within $\epsilon/(3(b-a))$ of $M_k$ and is guaranteed to not be larger than $N_k$, showing the inequality in your post is correct. If $N_k\leq M_k$ just do the logic in the other direction

 

[pasmith]

We have for $n > N$ that (dropping the constant multiple of $\epsilon$) $|f_n(x) - f(x)| < \epsilon$. We can write this in the following two ways: $$\begin{split} f_n(x) - \epsilon &< f(x) < f_n(x) + \epsilon \\ f(x) - \epsilon &< f_n(x) < f(x) + \epsilon. \end{split}$$ Ignoring the lower bounds and making the right hand sides as large as possible, we find that on the particular subinterval $$\begin{split} f(x) &< f_n(x) +\epsilon \leq N_k + \epsilon \\ f_n(x) &< f(x) + \epsilon \leq M_k + \epsilon.\end{split}$$ Now the first tells us that $N_k + \epsilon$ is an upper bound for $f(x)$, so that $$M_k \leq N_k + \epsilon.$$ Simiilarly the second tells us that $M_k + \epsilon$ is an upper bound for $f_n(x)$ so that $$N_k \leq M_k + \epsilon.$$ Putting these two inequlities together gives $$|N_k - M_k| \leq \epsilon$$ as required.