xtimmyx
- 5
- 0
Right angle force on "perfectly stretched string"
I have a theory which although physically impossible I would like to know some sort of answer to.
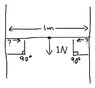
Image a string stretched between two trees. The string is perfectly stretched, totally horizontal, and has no elasticity, but can bend as a normal string.
My theory is that when a vertical force is applied to the middle of the string, no matter the size, the horizontal force upon the trees from the string is infinite. Or impossible to calculate.
I know that there is no such thing as a totally inelastic string and so on, but what would physics be without "what if´s"? :)
I've attached a picture of the problem with some units to it if someone would like to calculate it.
I have a theory which although physically impossible I would like to know some sort of answer to.
Image a string stretched between two trees. The string is perfectly stretched, totally horizontal, and has no elasticity, but can bend as a normal string.
My theory is that when a vertical force is applied to the middle of the string, no matter the size, the horizontal force upon the trees from the string is infinite. Or impossible to calculate.
I know that there is no such thing as a totally inelastic string and so on, but what would physics be without "what if´s"? :)
I've attached a picture of the problem with some units to it if someone would like to calculate it.