Rigid Bodies/ Angular Velocity

[WhiteWolf98]

Homework Statement

Homework Equations

$v=\omega r$

The Attempt at a Solution

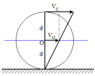
So, using the equation, one can work out the velocity at point $B$.
$v_B=\omega_{AB} \cdot r_B$
$v_B=6(0.4)=2.4~ ms^{-1}$I then tried working out the angular velocity at point $C$ using the instantaneous centre of zero velocity (I'm not sure of this is the correct next step. I don't think it is). But this ends up giving:
$\cos60= \frac {0.6} {r_{B/IC}}$
$r_{B/IC}=1.2$

Using $v=\omega r$, this gives the angular velocity at point $C$ as $2~rad/s$. This can't be right though since the velocity comes out as $0.2$ using $r=0.1~m$

The answer is $1.04~ms^{-1}$

 

[haruspex]

I then tried working out the angular velocity at point C using the instantaneous centre of zero velocity

Not sure what that means, or how you got the next equation.
Think about the velocity of C. What is the relationship between that and B's velocity?

 

[WhiteWolf98]

Could it be that $v_C={v_B} \cos30$?

 

[haruspex]

Could it be that $v_C={v_B} \cos30$?

Quite so.

 

[WhiteWolf98]

How can I use the velocity at point $C$ to work out the velocity at the centre of the gear?

 

[gneill]

How can I use the velocity at point $C$ to work out the velocity at the centre of the gear?

When in doubt, make a quick sketch: