- #1
fluidistic
Gold Member
- 3,923
- 261
Homework Statement
There's a problem that I don't even know really where to start. It seems extremely complex to me.
Basically there's a reverted cone of mass M with a mass of mass m that can slides over it without friction. But there's a constraint of motion for the particule, it must stay on a trail over the cone, of step L. The cone is totally free to rotate (it's on a frictionless surface). The system is put under the gravitational field.
1)Express the velocity of the particule with respect to an inertial system.
2)Write down the Lagrangian and the conserved quantities.
Homework Equations
Not sure.
The Attempt at a Solution
First of all the center of mass of the cone will move and its axis of rotation too (I think). So that it looks like extremely difficult to decide where to put my coordinate system. Let's say I put the original of my coordinate system on a point on the ground. Now I don't know what coordinate system is more appropriated since I'm dealing with a cone. Let's take cylindrical coordinates [itex](r, \theta, z)[/itex]. I don't know how to proceed further. :(
What should I do here?
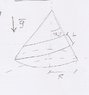
 , but my guess is that the question intends that it is only free to rotate (not free to translate) …
, but my guess is that the question intends that it is only free to rotate (not free to translate) …