- #1
Telemachus
- 835
- 30
I wanted to solve the problem of a cone rotating on its side over a table, around an axis that pass through it's apex, like in the figure.
What I want to find is the angular speed ω, the spin of the solid, such that the cone "stands" over it's apex. I don't know how to set the condition needed. Some how the normal force, at first distributed over the line, will be all applied at the apex when this happens. I can find the kinetic energy and the equations of movement for the cone, but I don't know how to find the angular speed required.
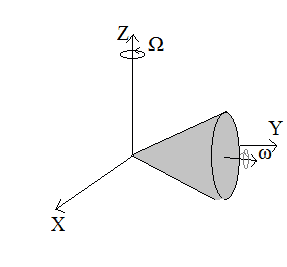
What I want to find is the angular speed ω, the spin of the solid, such that the cone "stands" over it's apex. I don't know how to set the condition needed. Some how the normal force, at first distributed over the line, will be all applied at the apex when this happens. I can find the kinetic energy and the equations of movement for the cone, but I don't know how to find the angular speed required.