RL Circuit Initial Current Simplification

[annamal]

Homework Statement

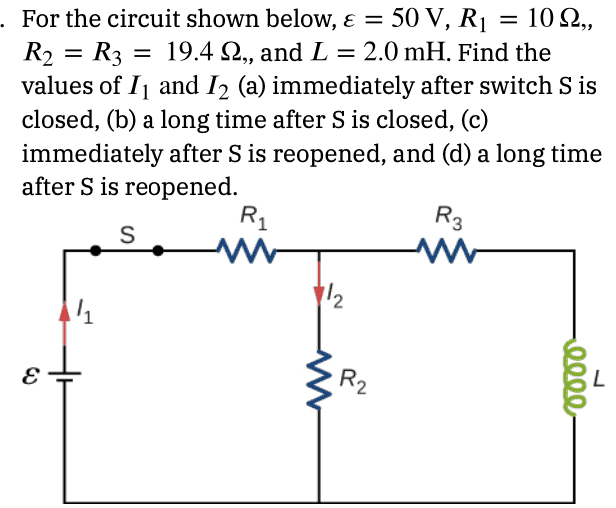
For the circuit shown below, v = 50 V, R1 = 10 ohms, R2 = R3 = 19.4 ohms, and L = 2 mH. Find the values of I1 and I2 (c) immediately after S is reopened

Relevant Equations

$\frac{LdI_3}{dt} + I_2 R_3 + I_2 R_2 = 0$
$I_2 = \frac{V}{R_3 + R_2}e^{-t/\tau}$

$I_2 = \frac{V}{R_3 + R_2}e^{-t/\tau}$
$I_2 = \frac{50}{19.4(2)}e^{-t/\tau}$ as t goes to 0, $I_2 = \frac{50}{19.4(2)}$ = 1.29 Amps which is not the answer.

 

[Orodruin]

First of all, what is your reason for using that formula? Please motivate.

Also, how are $I_3$ and $I_2$ related? What is your definition of $I_3$?

 

[Delta2]

I think you do a similar mistake here as the one at the other thread (where you used $\frac{\mathcal{E}}{R}$ instead of $\frac{\mathcal{E}}{2R}$)

For (c) that is immediately after S is reopened $I_1$ drops to zero and $I_2$ becomes equal to $I_3$.
$I_3$ can not change instantly because it is the current through the inductor, while we can make the assumption that the current through $R_1$ and $R_2$ can change instantly.

P.S As $I_3$ I refer to the current through the inductor (and $R_3$) immediately before we commit action (c). That is the current through the inductor at the end of (b).

 

[Orodruin]

For (c) that is immediately after S is reopened I1 drops to zero and I2 becomes equal to I3.

OP has not yet defined $I_3$. There is the matter of the sign if defined in the more canonical way. If so, $I_3 \neq I_2$.

 

[Delta2]

OP has not yet defined $I_3$. There is the matter of the sign if defined in the more canonical way. If so, $I_3 \neq I_2$.

This is interesting, can't wait for the OP to reply, so let's just say that $I_3$ is as I define it in my PS post #3.

 

[Orodruin]

This is interesting, can't wait for the OP to reply, so let's just say that $I_3$ is as I define it in my PS post #3.

That PS can be read as not necessarily specifying direction. I would say the canonical way would be to specify it as positive when the current goes from left to right through $R_3$. Then clearly $I_2 = - I_3$ when the switch is off by Kirchhoff’s current law in the upper vertex (or lower).

 

[Delta2]

Hmm sorry the truth is I am not expert in circuit theory so never heard of this "canonical way" of defining currents.

 

[Orodruin]

Hmm sorry the truth is I am not expert in circuit theory so never heard of this "canonical way" of defining currents.

I am just using canonical with its meaning of typical standard.

 

[Delta2]

Hmm, this seems to me as a subtlety of no real consequence towards solving this problem but yes I think you are right after all, under proper definition of $I_3$ and $I_2$ it can be $I_2=-I_3$.

 

[Orodruin]

I mean, not to give away too much, but one will have to deal with a minus sign somewhere.

 

[Delta2]

Well yes ok, after reconsidering a bit , it is a subtlety of some consequence, the direction of $I_2$ is going to be reversed relative to what it is at the end of (b) and we have to express this in some way.

It is just me I am always thinking of currents as positive quantities in circuit theory. I ll have to review that.

 

[DaveE]

It is just me I am always thinking of currents as positive quantities in circuit theory. I ll have to review that.

It's just you, and not for much longer, I'd guess. Yes, you need to get past that ASAP.

 

[annamal]

First of all, what is your reason for using that formula? Please motivate.

Also, how are $I_3$ and $I_2$ related? What is your definition of $I_3$?

It says so in my book. $I_3 = I_2$. Instead of I, we substitute for $I_2$

 

[Orodruin]

It says so in my book. $I_3 = I_2$. Instead of I, we substitute for $I_2$

View attachment 301753

This does not answer my question.

 

[annamal]

This does not answer my question.

Which part is unanswered?

 

[Orodruin]

Which part is unanswered?

What is your definition of I3?

 

[DaveE]

That PS can be read as not necessarily specifying direction. I would say the canonical way would be to specify it as positive when the current goes from left to right through $R_3$. Then clearly $I_2 = - I_3$ when the switch is off by Kirchhoff’s current law in the upper vertex (or lower).

I personally don't think there is a "canonical" way to assign polarities to voltages and currents in circuit analysis. However, every EE that does this has their own biases, like sources on the left and loads on the right. Currents flow left to right or clockwise in loops, voltages are more positive near the top, the passive sign convention, currents always flow into I/O ports, etc. The problem is that it doesn't take a very complex network before these rules fail, or, just don't seem simple.

One of the biggest error sources in circuit solutions is being confused about the polarity definitions and sign errors in the equations. I think the idea that there is a "right way" to define things actually makes this problem worse. It tempts people to think they don't have to worry about polarities or to make assumptions about the normal way it looks. A common problem is people trying to guess the answer to avoid negative values in their equation by defining things "the right way".

I think you are much better off to just understand up front the these assignments are COMPLETELY ARBITRARY, or could be. You always have to worry about this; you always have to write down your polarity definitions and refer back to them, you always have to TELL THE OTHER GUY what they are.

 

[Orodruin]

I think the idea that there is a "right way" to define things actually makes this problem worse.

I never claimed that there was a "right way", just that most people probably would assign $I_3$ to be the current going in the right direction (as in directional right, not as in being right right) through $R_3$.

you always have to write down your polarity definitions and refer back to them, you always have to TELL THE OTHER GUY what they are.

Which is exactly why I asked OP for this clarification.

A common problem is people trying to guess the answer to avoid negative values in their equation by defining things "the right way", for example.

This is not unique to circuit theory. The same holds true in classical mechanics when people start drawing their forces. The good thing is that they will just come out negative if one assumes wrong regarding the sign.

The physical fact is that $I_2$ in (c), as defined in the image in the OP, will be negative regardless of how one defines $I_3$.

 

[annamal]

What is your definition of I3?

I3 = I2

 

[DaveE]

This is not unique to circuit theory. The same holds true in classical mechanics when people start drawing their forces. The good thing is that they will just come out negative if one assumes wrong regarding the sign.

Yes. I think it's a common point of confusion to students new to linear systems. We would all do well to stress to them that polarity definitions don't require you to know the answer in advance. I hear students getting stuck worrying about which to choose when it doesn't matter. If you want your arrows to point the right way, redraw them after you've solved it. I think students get mixed messages when the symbols are used in other contexts to show the actual direction of things like electrons, fields, etc. But in analysis, they are just a way to generate a consistent set of equations, nothing more.

 

[SammyS]

What is your definition of $I_3$?

I₃ = I₂

I'm quite sure, that really is not the sort of definition @Orodruin is looking for.

Assuming that I₃ is the current flowing through resistor R₃, in what direction is it assumed to be flowing?

 

[alan123hk]

What is your definition of I3?

I3 = I2

There seems to be a bit problem with this definition. Why define a $I_3$ if it is always equal to $I_2$?
Why not just use the original $I_2$, isn't it simpler and more convenient?

If $I_3$ is not always equal to $I_2$, e.g. $I_3=I_2$ only after the switch $S$ is reopeoned, we cannot define that $I_3 \cong I_2$, the position and direction of $I_3$ should be accurately marked on the circuit to avoid misunderstanding, although we might be able to infer the direction of $I_3$ from the relationship.

Edit : But you also didn't explicitly say that $I_3$ is equal to $I_2$ only after the switch is reopened.

Say you're running a business and communicating with customers. If it is not expressed clearly according to the established method, it will cause many problems.

 

[Steve4Physics]

Here's an alternative approach.

The times of interest are the initial times (‘t=0’) and the steady-state times (‘t = ∞’). As a consequence, the questions are easily answered by understanding and applying three key facts about how an inductor behaves in a DC circuit like the one given:

1. For an ‘uncharged’ inductor, when the applied voltage changes suddenly, the inductor behaves (for an instant) as an infinite resistance (open circuit).

2. When the charging inductor reaches its steady state, it has zero voltage across it and a constant current (call it I₀) through it. The inductor acts as a zero resistance.

3. When the charged (steady-state) inductor discharges, the initial current through it is I₀ (as defined in point 2 above) and the final current through it is 0 (assuming no other sources are present).

If the above facts are applied, the questions can be easily answered without any differential equations. In fact this approach makes it obvious that the answers don’t even depend on the value of L!

Of course, the above approach won’t work for problems requiring currents at arbitrary specified times.

Can I also add to what @alan123hk said. The question does not ask for I₃. There is no reason to define it. The question asks only for I₁ and I₂ at key times. Using Kirchhoff’s 1st law, the current through R₃ and L (if required) is easily expressed in terms of I₁ and/or I₂ at the key times.

 

[alan123hk]

Can I also add to what @alan123hk said. The question does not ask for I₃. There is no reason to define it. The question asks only for I₁ and I₂ at key times. Using Kirchhoff’s 1st law, the current through R₃ and L (if required) is easily expressed in terms of I₁ and/or I₂ at the key times.

Yes, it's not necessary to define $I_3~$, but if the problem solver wants to define another variable $I_3~$, that's fine too.
The problem now seems to be that OP mentioned a differential equation $\frac{LdI_3}{dt} + I_2 R_3 + I_2 R_2 = 0~$ involving $I_3$ in the first post, but he didn't explain clearly what it was, so it might confuse many people trying to follow his ideas to help.

 

[annamal]

Yes, it's not necessary to define $I_3~$, but if the problem solver wants to define another variable $I_3~$, that's fine too.
The problem now seems to be that OP mentioned a differential equation $\frac{LdI_3}{dt} + I_2 R_3 + I_2 R_2 = 0~$ involving $I_3$ in the first post, but he didn't explain clearly what it was, so it might confuse many people trying to follow his ideas to help.

I meant $\frac{LdI_2}{dt} + I_2 R_3 + I_2 R_2 = 0$ if that makes it clearer since I2 = I3. When I solve this differential equations, $I_2 = \frac{V}{R_3 + R_2}e^{-t/\tau}$, but as t goes to 0, I2 = 1.29 amps which is not the answer.

 

[alan123hk]

I meant LdI2dt+I2R3+I2R2=0 if that makes it clearer since I2 = I3. When I solve this differential equations, I2=VR3+R2e−t/τ, but as t goes to 0, I2 = 1.29 amps which is not the answer.

Ok, you mentioned in your first post that you were just focusing on finding an answer to question c ( immediately after S is reopened), which I seem to have missed.

Then we need to know what is the steady-state current of the inductor after the switch is closed for a long time, and this value is obviously not equal to $\frac{V}{R_3 + R_2}=\frac{50}{19.4(2)}=1.29$

 

[Delta2]

I meant $\frac{LdI_2}{dt} + I_2 R_3 + I_2 R_2 = 0$ if that makes it clearer since I2 = I3. When I solve this differential equations, $I_2 = \frac{V}{R_3 + R_2}e^{-t/\tau}$, but as t goes to 0, I2 = 1.29 amps which is not the answer.

You used wrong initial condition when solving the ODE. It is NOT $$I_2(0)=\frac{V}{R_3+R_2}$$ rather it is $I_2(0)=$the current the inductor has at the end of (b) (that is immediately before (c) happens).

 

[kuruman]

Why define a $I_3$ if it is always equal to $I_2$?

Not "always". The two currents are not equal after the switch is closed in part (a). They become equal when a "long time" has elapsed.

 

[annamal]

You used wrong initial condition when solving the ODE. It is NOT $$I_2(0)=\frac{V}{R_3+R_2}$$ rather it is $I_2(0)=$the current the inductor has at the end of (b) (that is immediately before (c) happens).

I'd like to focus only on part c).
Why not? the L, R2, and R3 components are what makes the circuit after the circuit is immediately opened.

 

[Delta2]

I'd like to focus only on part c).
Why not? the L, R2, and R3 components are what makes the circuit after the circuit is immediately opened.

The ODE you formed(at post #25) is correct. The general solution to that ODE is $$I(t)=Ce^{-t/\tau}$$ where $$\tau=\frac{L}{R_2+R_3}$$.

Now to determine the constant C you use as initial condition $$I(0)=\frac{V}{R_2+R_3}$$. I am going to throw the little ball to you now (direct translation from Greek idiomatic phrase e hehe). Please elaborate why you think that the initial current of inductor is that i.e $\frac{V}{R_2+R_3}$, I mean, the voltage source V is detached from the loop when (c) happens, I really don't understand you here.

 

[alan123hk]

Not "always". The two currents are not equal after the switch is closed in part (a). They become equal when a "long time" has elapsed.

Yes, it does, because $R_2=R_3$

Another interesting thing is that after removing the battery, according to the OP's statement $I_3=I_2~$, $I_3$ needs to be defined as the opposite direction.

 

[Delta2]

Oops now I noticed that $R_2=R_3$, however I think $I_2(0)\neq\frac{V}{R_2+R_3}$, $R_1$ should feature in $I_2(0)$ too besides $R_2,R_3$.

 

[annamal]

Oops now I noticed that $R_2=R_3$, however I think $I_2(0)\neq\frac{V}{R_2+R_3}$, $R_1$ should feature in $I_2(0)$ too besides $R_2,R_3$.

But no current flows through R1...?

 

[Delta2]

Good argument but still you are wrong. Hold on why I explain why.

 

[Delta2]

What is the current through the inductor right before event (c)? Does $R_1$ feature in that? Can that current change instantly to $\frac{V}{R_2+R_3}$ right after event (c)?

 

[annamal]

What is the current through the inductor right before event (c)? Does $R_1$ feature in that? Can that current change instantly to $\frac{V}{R_2+R_3}$ right after event (c)?

So is R2 parallel to R1? R1' = 1/[(1/R2) + (1/R1)], Rtotal = R1' + R3; if I(0) = V/(Rtotal) that does not give the correct current either

 

[Orodruin]

I find it remarkable that after an entire page of posts the OP still refuses to define the direction of his currents. Without properly taking current directions into account and with just handwaving arguments like ”currents have to be the same” without any reference to current direction, we will not progress.

Another fundamental fact that the OP ignores is that current through an inductor changes continuously. This is the same type of issue that was treated in another of OP’s recent threads.

It is unclear why the OP believes that the initial current should be $V/(R_2+R_3)$. Yes, the closed loop only contains R2 and R3 after the switch opens, but it does not contain the EMF.

 

[Orodruin]

So is R2 parallel to R1? R1' = 1/[(1/R2) + (1/R1)], Rtotal = R1' + R3; if I(0) = V/(Rtotal) that does not give the correct current either

No. You need to review how inductors behave in the short and long term limits. In the short term an inductor keeps its current (including the current direction!) and in the long term it acts as a perfect conductor (as long as we are only considering direct currents).

Allegedly you have already answered (b). What is the current through the inductor in (b) and why? This current will not change directly after opening the switch. What does this tell you about $I_2$ right after opening the switch?

 

[Delta2]

So is R2 parallel to R1? R1' = 1/[(1/R2) + (1/R1)], Rtotal = R1' + R3; if I(0) = V/(Rtotal) that does not give the correct current either

Seems our brains are in different "phase" here . Please calculate $R_{total}$ with the circuit configuration as it is at the end of (b), that is before the switch reopens and when inductor acts as a short circuit (or as a perfect conductor if you prefer that).

 

[alan123hk]

So is R2 parallel to R1? R1' = 1/[(1/R2) + (1/R1)], Rtotal = R1' + R3; if I(0) = V/(Rtotal) that does not give the correct current either

You seem to be trying to apply Thevenin's theorem, but you don't know how to calculate Thevenin's equivalent voltage.

Anyway, I believe you should agree that the current should not change anymore after the circuit has had enough time to stabilize, at which point the inductor can be considered a perfect conductor, you can do the calculations with a very simple circuit, that is a resistor (R1) is in series with two parallel resistors (R2 and R3), so you should be able to easily find the desired inductor initial current.

 

[bhobba]

This reminds me of a question you would get in an applied differential equations course. All you really have to do is make a reasonable assumption about I3 such that I1 = I2 + I3.

Suppose the switch is open and the circuit has settled down. The inductor is then a dead short so R2 and R3 are effectively connected in parallel and there is no current or voltages across the resistors ie I1, I2, I3 = 0. If the switch is closed again then after it has settled down the inductor is a dead short and currents are easily calculated.

When the switch is instantaneously open or closed the current in the inductor changes creating a voltage so the currents are more difficult to calculate. If the switch is closed V = I2*R2 = I3*R3 + L dI3/dt where V is the voltage across R2. When the switch is closed it is a step function F(t) of zero before t=0 and 50V after t=0. F(t) = I1*R1 + I2*R2 and F(t) = I1*R1 + I3*R3 + L dI3/dt. This second equation is a first-order differential equation that can be solved in a number of ways eg Laplace Transforms.

You express everything in terms of I2 and I3, take Laplace transforms and solve the resulting simultaneous equations. When reopened F(t) = 50v at before t=0 and zero after t=0. In the tradition of our forum where we believe in guiding posters rather than doing all the work that should be enough for the OP to solve the problem.

Thanks
Bill

 

[Orodruin]

When the switch is instantaneously open or closed the current in the inductor changes creating a voltage so the currents are more difficult to calculate. If the switch is closed V = I2*R2 = I3*R3 + L dI3/dt where V is the voltage across R2. When the switch is closed it is a step function F(t) of zero before t=0 and 50V after t=0. F(t) = I1*R1 + I2*R2 and F(t) = I1*R1 + I3*R3 + L dI3/dt. This second equation is a first-order differential equation that can be solved in a number of ways eg Laplace Transforms.

There is no need to solve differential equations to answer the questions being asked here. All you need to know is that on large times, the inductor acts like a short circuit and on small times the current through it remains the same (ie, it needs to change continuously).

 

[DaveE]

You express everything in terms of I2 and I3, take Laplace transforms and solve the resulting simultaneous equations. When reopened F(t) = 50v at before t=0 and zero after t=0. In the tradition of our forum where we believe in guiding posters rather than doing all the work that should be enough for the OP to solve the problem.

Yes, but guiding them to use advanced techniques that they are unlikely to understand in an unnecessary effort to solve everything about the circuit response may not be very helpful.

Key point: everything about this question happens at t=0.

 

[Steve4Physics]

Yes, but guiding them to use advanced techniques that they are unlikely to understand in an unnecessary effort to solve everything about the circuit response may not be very helpful.

100% agree. The solution to the original question is (using the right approach) almost trivial and requires only basic arithmetic. But it needs an intuition about how inductors behave (Post #23).

Key point: everything about this question happens at t=0.

I would add, also at t= ∞.

 

[alan123hk]

Differential equations are used when we need to find the transient response of an LCR circuit.

 

[annamal]

I find it remarkable that after an entire page of posts the OP still refuses to define the direction of his currents. Without properly taking current directions into account and with just handwaving arguments like ”currents have to be the same” without any reference to current direction, we will not progress.

Sorry if I didn't answer your questions clearly. The directions of I2 and I3 are below. I3 = I2 when the switch is open

Another fundamental fact that the OP ignores is that current through an inductor changes continuously. This is the same type of issue that was treated in another of OP’s recent threads.

Yes, I know that. That's why in my first post I have $\frac{LdI_2}{dt} + I_2 R_3 + I_2 R_2 = 0$ where that is kirkoff's loop laws for the I2 circuit with the inductor, solving for I2, we have $I_2 = \frac{V}{R_3 + R_2}e^{-t/\tau}$ where I2 is the current going through the inductor

It is unclear why the OP believes that the initial current should be $V/(R_2+R_3)$. Yes, the closed loop only contains R2 and R3 after the switch opens, but it does not contain the EMF.

What should the initial current be then?

 

[DaveE]

Sorry if I didn't answer your questions clearly. The directions of I2 and I3 are below. I3 = I2 when the switch is open

Do you understand the concept of polarity? |I₂| = |I₃| isn't the same as I₂ = I₃.
In your diagram if I₂ = I₃ then (by KCL) the current through R1 must be I₂ + I₃, which will be hard to achieve if the switch is open.
It looks to me, from your diagram that I₂ + I₃ = 0 thus I₂ = -I₃ when the switch is open.

 

[annamal]

Do you understand the concept of polarity? |I₂| = |I₃| isn't the same as I₂ = I₃.
In your diagram if I₂ = I₃ then (by KCL) the current through R1 must be I₂ + I₃, which will be hard to achieve if the switch is open.
It looks to me, from your diagram that I₂ + I₃ = 0 thus I₂ = -I₃ when the switch is open.

Yes I2 = -I3...wondering if you could help me solve the problem from here...

 

[Delta2]

Just wondering is the answer key for (c) 2.54A?

 

[Orodruin]

Yes, I know that. That's why in my first post I have LdI2dt+I2R3+I2R2=0 where that is kirkoff's loop laws for the I2 circuit with the inductor, solving for I2, we have I2=VR3+R2e−t/τ where I2 is the current going through the inductor

You are completely missing the point.

First of all, getting the correct differential equation is not sufficient to accurately describe the system. You also need to find the correct initial conditions, which is where you are failing. Second, (c) is a question about the initial condition so the actual differential equation is irrelevant to solving (c).

What should the initial current be then?

You tell me: How did you arrive at that initial condition? What is the logical steps you took to deduce it? You have been here long enough to know that we are not in the habit of just telling you the answer.

Yes I2 = -I3...wondering if you could help me solve the problem from here...

People have been doing nothing else than trying to help you for almost 50 posts. Adding a dismissive attitude on top of refusing to define your variables for an entire page is not going to increase people’s willingness to help you.