RMS and average current triangle

[billy fok]

I would like to know how to find RMS and average current of a triangle?
i searched the web. but it focus from 0. which i know.
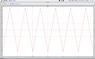
but my waveform is different from the internet. i have attached the waveform..
Maximum = 2.5 , Minimum = 1.8

i need to find out the RMS and average current

 

[donpacino]

http://en.wikipedia.org/wiki/Root_mean_square
think about what RMS stands for, then think how your final answer will be derived

 

[Babadag]

Following the definition:

"The RMS over all time of a periodic function is equal to the RMS of one period of the function."

And :

frms=sqrt[integral(f(t)^2/T]

f(t)up=yo+(y1-yo)/(x1-xo)*(x-xo) integrated for x=x1 and x=xo

f(t)down=y1-(y1-yo)/(x1-xo)*(x-x1) for x=2*x1 and x=x1

where T=0.05 xo=0;x1=T/2;yo=1.8;y1=2.5

frms=sqrt{[integral(f(t)up^2+integral(f(t)down^2]/T}

integral(f(t)up^2=aup*x+bup*x^2/2+cup*x^3/3 x=x1 and x=xo

integral(f(t)down^2=adown*x+bdown*x^2/2+cdown*x^3/3 x=2*x1 and x=x1

Let's put k= (y1-yo)/(x1-xo).Then:

aup=yo^2-2*k*yo*xo+k^2*xo^2

bup=2*yo*k-2*xo*k^2

cup=k^2

adown=y1^2+2*y1*k*x1+k^2*x1^2

bdown=-2*y1*k-2*k^2*x1

cdown=k^2

frms=2.16[approx.]

 

[NascentOxygen]

i need to find out the RMS and average current

What have you calculated as its average value?

 

[Babadag]

Following:

http://en.wikipedia.org/wiki/Average

AM=1/n*Sum[y(i)]|y(1)=yo to y(n)=y1

Let's take n number of equal distanced points on upright part of the triangle.The number of intervals

will be n-1.Each y[y(i)] value will be y(i)=yo+(i-1)*(yn-yo)/(n-1)

Sum[y(i)]|y(1)=yo to y(n)=y1=n*yo+ (y1-yo)/(n-1)*Sum(1+2+3+..n-1)

Sum(1+2+3+..n-1)=n*(n-1)/2. Then:

Sum[y(i)]|y(1)=yo to y(n)=y1=n*yo+n*(n-1)/2*(y1-yo)/(n-1)=n*yo+n/2*(y1-yo)

AM=1/n*Sum=yo+(y1-yo)/2=(y1+yo)/2

AM=(1.8+2.5)/2=2.15