- #1
tworitdash
- 104
- 25
I want to simulate the time domain data for a rotating radar. I assume that the space around the radar is filled up with a very big extended object and it moves with a constant speed in one direction. Picture attached.
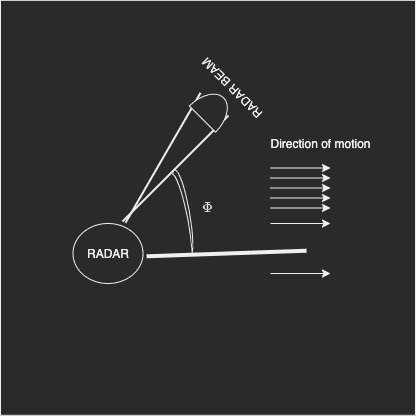I don't take range information here. I am only concerned about the velocity as in all ranges I consider the velocity to be constant.
My approach:
I consider first when the radar is not rotating and it is directed at ϕ=0 (exactly the same direction of the motion of the target). In that case, the time domain data looks like the following.<br /> s(t) = e^{j \frac{4\pi}{\lambda }\mu t}<br />
Where \mu is the velocity of the target. The term \lambda is the wavelength of the radar.
If I observe the phase of this signal carefully, it is just an integral over the velocity with respect to time.
$$
Phase(s(t)) \propto \int \mu dt
$$
This way I did my thought experiment. If I see the target from a rotating radar, the radial velocity I receive from different directions in space would have a cosine dependence.
$$
v_r(t) = cos(\phi(t)) \mu
$$
Here v_r is the radial velocity that radar receives. The term \phi(t) is a function of t and the rotation speed \Omega . This is basically the angle subtended by the radar beam with the target motion direction at a given time.
$$
\phi(t) = \phi_{target} - (\Omega t + \phi_0)
$$
Where \phi_0 is the initial angle of observation and \phi_{target} is the target motion direction.
Keeping this in mind I performed the following integral
$$
\int cos(\phi(t)) \mu dt
$$
Which is
$$
\frac{-1}{\Omega} sin(\beta_{target} - (\Omega t + \phi_0))
$$
So, my time-domain data becomes,
$$
s(t) = e^{j \frac{-4\pi}{\lambda \Omega} sin(\beta_{target} - (\Omega t + \phi_0))}
$$
I did one simulation with the target motion direction as \phi_{wind} = 0 and \phi_0 = 0 . I have data for the entire rotation and I plot a micro-doppler spectrogram. I have 167\times360 points for one rotation. So, I do Doppler FFT processing for every one degree of \phi (167 points DFT) and plot it. Figure attached.
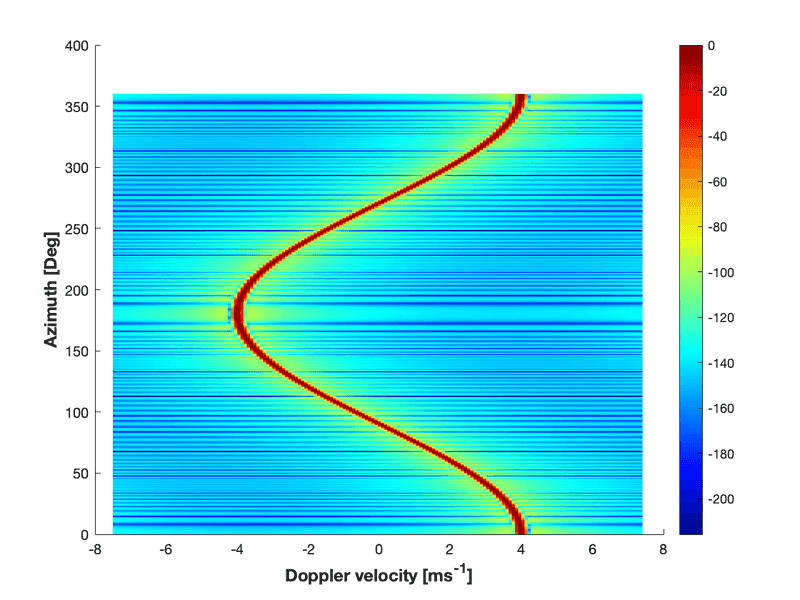
Although it looks correct, I need a second eye who verifies my process here and if I am doing it alright physically. Physically radar receives the radial velocity and with that in mind, I formulated the phase of the time domain signal.
My approach:
I consider first when the radar is not rotating and it is directed at ϕ=0 (exactly the same direction of the motion of the target). In that case, the time domain data looks like the following.<br /> s(t) = e^{j \frac{4\pi}{\lambda }\mu t}<br />
Where \mu is the velocity of the target. The term \lambda is the wavelength of the radar.
If I observe the phase of this signal carefully, it is just an integral over the velocity with respect to time.
$$
Phase(s(t)) \propto \int \mu dt
$$
This way I did my thought experiment. If I see the target from a rotating radar, the radial velocity I receive from different directions in space would have a cosine dependence.
$$
v_r(t) = cos(\phi(t)) \mu
$$
Here v_r is the radial velocity that radar receives. The term \phi(t) is a function of t and the rotation speed \Omega . This is basically the angle subtended by the radar beam with the target motion direction at a given time.
$$
\phi(t) = \phi_{target} - (\Omega t + \phi_0)
$$
Where \phi_0 is the initial angle of observation and \phi_{target} is the target motion direction.
Keeping this in mind I performed the following integral
$$
\int cos(\phi(t)) \mu dt
$$
Which is
$$
\frac{-1}{\Omega} sin(\beta_{target} - (\Omega t + \phi_0))
$$
So, my time-domain data becomes,
$$
s(t) = e^{j \frac{-4\pi}{\lambda \Omega} sin(\beta_{target} - (\Omega t + \phi_0))}
$$
I did one simulation with the target motion direction as \phi_{wind} = 0 and \phi_0 = 0 . I have data for the entire rotation and I plot a micro-doppler spectrogram. I have 167\times360 points for one rotation. So, I do Doppler FFT processing for every one degree of \phi (167 points DFT) and plot it. Figure attached.
Although it looks correct, I need a second eye who verifies my process here and if I am doing it alright physically. Physically radar receives the radial velocity and with that in mind, I formulated the phase of the time domain signal.
