Rotating rod and forces

[Vivek98phyboy]

Homework Statement

A uniform rod of length L pivoted at its upper end hangs vertically. It is displaced through an angle of 60° and then released. Find the magnitude of the force acting on a particle of mass 'dm' at the tip of the rod when the rod makes an angle of 37° with the vertical.

Relevant Equations

Tangential acceleration of tip(dm), a= L𝛂

After solving using energy conservation, I found the angular velocity at 37° to be omega=2.97/(L)^½

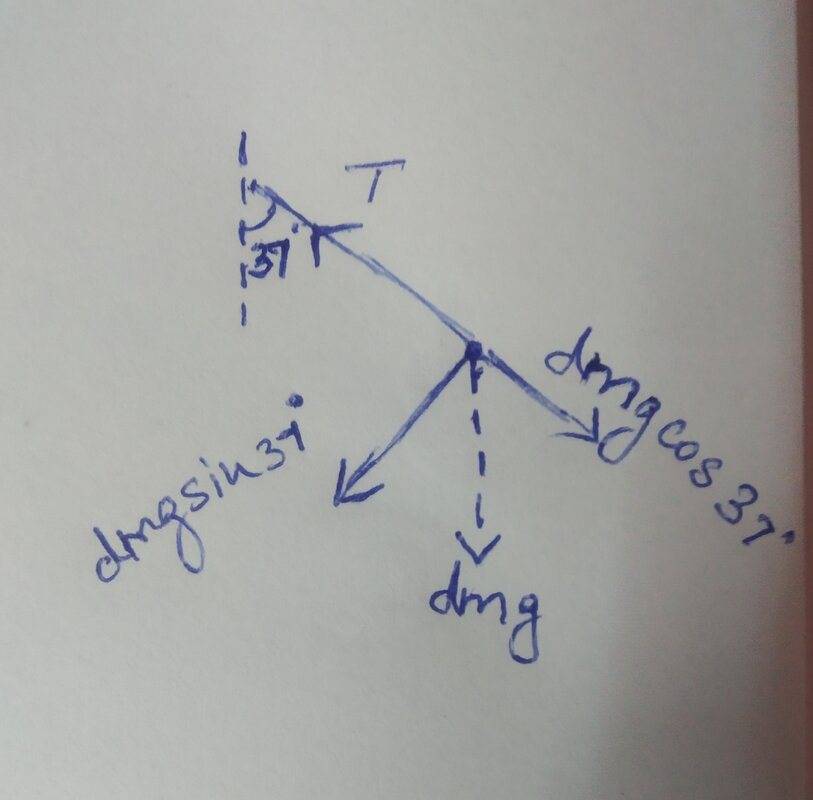
Tension and the weight (dm)g are the two forces acting on the tip dm
To find the resultant force, I resolved the centripetal force and tangential force to find the centripetal force as
F= (dm)(L)(omega)²
and tangential force as (dm)(g)sin37°.
This would leave me with a tangential acceleration of 5.9 m/s²
But when I calculated it using torque, I found the tangential acceleration to be 8.82m/s² and that is the solution given in my book

What am I doing wrong while resolving the forces?

I would also like to know what would be the forces provided by the part of rod that is above 'dm'?

 

[TSny]

The force of gravity is not the only force on $dm$ that has a tangential component. The force that "binds" $dm$ to the rod also has a tangential component.