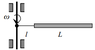Rotating rod - potential difference between the ends

[Rugile]

Homework Statement

A rod of length L and made of conducting material is attached with a smaller non-conducting rod of length l to an axle, which is rotating at constant angular velocity ω (see attachment). Find the potential difference between the ends of the rod. Of what strength magnetic field should be turned on in order to double the potential difference? The charge of electron is e, mass m.

Homework Equations

I = \int {r^{2} dm}

The Attempt at a Solution

No idea where to start! I don't even know how to calculate the moment of inertia - if we need it - because we don't have the mass of the rod. It's really confusing (since there is no magnetic field), and I really would appreciate a hint!

 

[Simon Bridge]

You don't need the moment of inertia - the rod is already turning.
The question supposes that just spinning the rod is enough to create a potential difference between the ends.
How do you think this would happen? (hint: what happens to the free charges in the conductor?)

 

[Rugile]

Is it like... centripetal force? Do the free charges create an electric field?

 

[Simon Bridge]

It is the centripetal/centrifugal stuff, yeah.

A conductor consists of fixed positive charges surrounded by free negative charges.
The negative charges experience a centrifugal effect. (They all do but the fixed charges can't move.)
This separates out the charges - producing the electric field.

The wording of the question suggests you have notes on this effect already.
Related thread:
https://www.physicsforums.com/showthread.php?t=626114

 

[Rugile]

So the negative free charges kind of go to one end of the rod? And then it produces the electric field going from these negative charges to fixed positive charges in the rod? The electric field is kind of distributed along the rod?

I can't really find any relevant notes..

 

[rude man]

So the negative free charges kind of go to one end of the rod? And then it produces the electric field going from these negative charges to fixed positive charges in the rod? The electric field is kind of distributed along the rod?

I can't really find any relevant notes..

You're half right. The electrons pile up on the outside part of the rod, leaving a net positive charge on the pivot side. But there is no net E field inside the rod. But think of the zero field as comprising two equal and opposite fields.

You have the right idea though and should be able to do part a now.

 

[Rugile]

Why is there no net field inside the rod?

For now, I think I can write Newton's law:

m \omega ^2 x = E*e, where e is electron's charge, m its mass and x is the distance to the axis of rotation. But if there is no net field, I'm lost...

 

[ehild]

You are right. In the stationary rod, there is no net electric field inside it and the electrons distribute homogeneously. In the rotating rod, the electron distribution changes, the centrifugal force pushes them outward, making the outside of the rod more negative then the central part. The electron distribution produces an electric field inside the rod. New equilibrium is established when the electric force balances the centrifugal force at each point of the rod, that is your equation holds. The next task is to find the potential difference between the ends of the rod.

ehild

 

[Rugile]

Okay, so I think I got this now :) we know that E = \frac{m \omega ^2 x}{e}, and the potential difference \Delta \phi = \int Edx = \int \frac{m \omega ^2 x}{e} dx. Integrate from l to L+l and that's it. It's correct, I hope?

 

[ehild]

It is correct, but a minus sign. $\Delta \phi = -\int Edx$

ehild

 

[rude man]

Okay, so I think I got this now :) we know that E = \frac{m \omega ^2 x}{e}, and the potential difference \Delta \phi = \int Edx = \int \frac{m \omega ^2 x}{e} dx. Integrate from l to L+l and that's it. It's correct, I hope?

I agree, and I wouldn't worry about the minus sign since the question did not ask for it explicitly.
Don't forget you still have a part (b)!