Rotation of Rigid Bodies: Rotating stick with disc on top

[Exath]

Homework Statement

[/B]
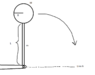
A thin cylindrical rod with the length of L = 24.0 cm and the mass m = 1.20 kg has a cylindrical disc attached to the other end as shown by the figure. The cylindrical disc has the radius R = 8.00 cm and the mass M 2.00 kg. The arrangement is originally straight up vertical), but it can fall and rotate around a frictionless axis. What is the arrangement's kinetic energy when it has rotated 90 degrees and is momentarily horizontal? What is the angular velocity and what is the velocity of the discs center of mass in this location? Compare this with what the velocity of the disc would have if the disc passed the line A if you had only dropped the disc straight down (without the rod).

Rod:
m = 1.2kg
L = 0.24m

Disc:
R = 0.08m
M = 2kg

Homework Equations

Inertia of the rod = 1/3*mL^2

Energy equation: U1 + K1 = U2 + K2

Kinetic energy of rotating rigid body: K = 1/2*mv^2 + 1/2*Iw^2 (w = angular velocity, I = Inertia)

The Attempt at a Solution

Pretty much stuck at the first part: Calculating the kinetic energy of the system when it reaches line A.

Started with the energy principles: U1 + K1 = U2 + K2. No kinetic energy at the start, K1 = 0, No potential energy at the end when it reaches line A because it momentarily stops according to the text: U2 = 0, This gives U1 = K2 so we only need to find the potential energy of the system. The potential energy of the disc is M*g*(L + R) (counting from center of mass). Not really sure how potential energy works for a rod rotating about an axis on one of its ends though.

The kinetic energy for a rotating rigid body is K = 1/2*mv^2 + 1/2*Iw^2, this becomes K2 = 1/2*Iw^2 (remove 1/2*mv^2 because there is no movement for this rigid body, only rotation). Here, I is the inertia of the entire system, which is the inertia of the rod (1/3*mL^2) plus the discs inertia. Now this is another problem. There is no formula for inertia for a disc spinning about an axis on its "edge". Maybe we could derive one with calculus, but that would be taking it too far... At one point i considered the disc as a single point meaning we could just use the general inertia formula m*r^2 for it, but that would also be going too far because a radius was given, it's clearly not meant to be just a point.

So we have U1 = K2 => (Potential rod + potential disc) = 1/2*(Inertia rod + Inertia disc)*w^2

with this i could solve the angular velocity w and then easily find the kinetic energy K2, but i have no idea what the potential energy for the rod is and inertia for the disc...

any ideas?

 

[Doc Al]

Started with the energy principles: U1 + K1 = U2 + K2. No kinetic energy at the start, K1 = 0, No potential energy at the end when it reaches line A because it momentarily stops according to the text: U2 = 0, This gives U1 = K2 so we only need to find the potential energy of the system. The potential energy of the disc is M*g*(L + R) (counting from center of mass).

So far, so good.

Not really sure how potential energy works for a rod rotating about an axis on one of its ends though.

Just like the disk. What happens to the center of mass of the rod?

 

[Doc Al]

There is no formula for inertia for a disc spinning about an axis on its "edge".

Look up the parallel axis theorem.

 

[Exath]

It also falls like the disk, but counting from the center of mass it would be m*g*(L/2)?

 

[Doc Al]

It also falls like the disk, but counting from the center of mass it would be m*g*(L/2)?

Exactly.

 

[Exath]

Ok, so what's left is the inertia for the disk, how would i go about finding that?

 

[Doc Al]

Ok, so what's left is the inertia for the disk, how would i go about finding that?

See my second post in this thread.

 

[Exath]

Ah, the inertia should be Icm + Md^2 (d = distance between new axis and center of mass) = 1/2*MR^2 + M*(R + L)^2

 

[Doc Al]

Ah, the inertia should be Icm + Md^2 (d = distance between new axis and center of mass) = 1/2*MR^2 + M*(R + L)^2

Excellent!

 

[Exath]

Excellent!

Thanks for the help i got the rest from there :D