Valerie Prowse
- 25
- 0
Homework Statement
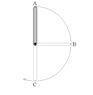
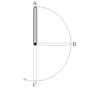
Consider a uniform rod of mass 12 kg and length l.0 m. At its end, the rod is attached to a fixed, friction-free pivot. Initially the rod is balanced vertically above the pivot and begins to fall (from rest) as shown in the diagram. Determine,
a. the angular acceleration of the rod as it passes through the horizontal at B.
b. the angular speed of the rod as it passes through the vertical at C.
Homework Equations
I = mr^2
KE(rotation)i = KE(rotation)f,
1/2Iω^2 + mgL = ...etc.
The Attempt at a Solution
I think I have it figured out, but I would just like to double check my answer as it's an assignment question.
I started with:
I (rod) = 1/3mL^2
L = 1.0m
m = 12kg
center of mass = L/2 = 0.5m
For a)
E0 = Ef
mg(L/2) = 1/2 (1/3mL2)ω2
(mgL)/2 = 1/6mL2ω2
ω = sqrt[(3g/L)] = 5.4 rad/s
For b)
I wasn't entirely sure how to go about this part without including some form of potential energy.. since rotational energy at point A would just = E at point C and everything would be the same?? I thought maybe since point C is below the axis of rotation that the center of mass would be located at -0.5m?
1/2Iω2 = 1/2Iω2 - (mgL/2)
(mL2ω2)/6 + (mgL)/2 = (mL2ω2)/6
ω2 (point C) = (mL2ω2 + 3mgL)/mL2
ω2 = (mL[Lω2+3g]/mL2) (L = 1)
ω = sqrt(ω2+3g)
ω = 7.65 rad/s
The answer does seem plausible to me, but I am not sure if my approach in adding mg(-L/2) to the KE in part B was correct. Any feedback is appreciated!