Rotational Mechanics question with spring

[Ujjwal Basumatary]

Homework Statement

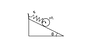
A uniform cylinder of mass $M$ and radius $R$ is released from rest on a rough inclined surface of inclined surface of inclination $\theta$ with the horizontal as shown in the figure. As the cylinder rolls down the inclined surface, what is the maximum elongation in the spring of stiffness $k$?

2. The attempt at the solution
Here is what I have thought about the problem:

We choose the origin to coincide with the equilibrium position of the spring, the x-axis along the incline and the y-axis perpendicular to it.

Let $a$ be the linear acceleration at an arbitrary instant of time. Also let $\alpha$ be the angular acceleration of the block at the same. Since there is no slipping, we have $a=R\alpha$.

The equation for tangential motion is, therefore $$Mg\sin\theta - kx-f=Ma$$

For angular motion, $$fR=I\alpha$$

Where,
$x =$ displacement from the origin
$g =$ acceleration due to gravity
$f =$ force of friction
$I =$ moment of inertia of the cylinder through its central axis

Substituting the value of $f$ from the second equation into the first, we obtain $$mg\sin\theta - kx- \frac{I\alpha}{R} = Ma$$

But at the extreme position, linear as well as tangential acceleration is zero. Substituting, $a=\alpha=0$ in the above we get $$x=\frac{Mg\sin\theta}{k}$$

But this is the elongation from the origin, and the spring was initially at $-x$. Therefore maximum elongation is given by$$x_{max} = \frac{2Mg\sin\theta}{k}$$

Am I correct in my reasoning? The answer is given to be this but I suspect I might have missed something in the middle as I am new to rotational mechanics. Any help would be appreciated. Thanks a lot.

 

[Orodruin]

It is a bit unclear to me what you mean by the spring's equilibrium position. You could mean one of two things:

• Where the system is at equilibrium.
• Where the spring is unstretched.

Your argumentation in the end seems to suggest the first, but your argumentation for the location of the zero-acceleration point seems to suggest the latter.

That being said, you could also just do an energy argument, which will avoid any rotational involvement altogether.

 

[Ujjwal Basumatary]

It is a bit unclear to me what you mean by the spring's equilibrium position. You could mean one of two things:

• Where the system is at equilibrium.
• Where the spring is unstretched.

Your argumentation in the end seems to suggest the first, but your argumentation for the location of the zero-acceleration point seems to suggest the latter.

That being said, you could also just do an energy argument, which will avoid any rotational involvement altogether.

I'm sorry for being unclear. I meant the position where the spring is unstretched.

 

[Orodruin]

Then that is where the contraption was released so

But this is the elongation from the origin, and the spring was initially at −x.

is not true. The spring was initially at $x = 0$. However, the point you have computed is not that where the system changes direction, it is where it has zero acceleration.

 

[Ujjwal Basumatary]

Then that is where the contraption was released so

is not true. The spring was initially at $x = 0$. However, the point you have computed is not that where the system changes direction, it is where it has zero acceleration.

I see that flaw. Thanks a lot for pointing it out. I found a better and neater solution.

The decrease in gravitational potential energy is equal to the increase in spring potential energy and hence we have $$mgx\sin\theta = \frac{1}{2}kx^2$$
Rearranging yields the answer. I hope this is correct :)