Undergrad Rubber Trapezoid and Righting Moment

[CptCavin]

TL;DR

Tipping Moment and Righting Moment of an object on a rubber platform.

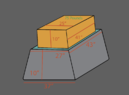
I am trying to understand how to find the righting moment of an inflatable trapezoid with 75-pounds at the top. The object at the top is 10" tall and weighs 75-pounds. The 75-pound weight will be fixed to the top of the inflatable trapezoid. The top and bottom of the trapezoid have rigid platforms glued to them post production of the inflatable trapezoid. The primary movement will not be a yaw in any direction but a bounce up and down movement.

I like math and all this but having a hard time to which rules and principles I should get familiar with before chatting with an engineer.

 

[Dale]

Is the inflatable trapezoid inflated enough that we can consider it rigid, or do we need to assume it will deform during tipping?

Also, is the result of this thing tipping over just going to be some inconvenience picking stuff up off the ground, or is a tipping event a hazard that risks harm to someone?

 

[CptCavin]

Great questions — It would deform and potentially tip, but it wont burst. The tipping event is a risk that would harm someone. I have a few ideas for a safety mechanism but still working that part...

 

[Lnewqban]

Welcome!

The whole thing needs to be turned over sideways beyond 51 degrees from the represented position in order to make it flip over.

Do you believe that the bouncing could take it to that extreme?

The following is a scaled drawing.

 

[Baluncore]

It would deform and potentially tip, but it wont burst.

Then one edge of the mass can sink into the inflated rubber trapezoidal envelope.
Any tilt of the mass will increase the force applied to that edge.
The mass can then roll off the rubber stand.
Internal pressure will be critical to stability.

 

[Chestermiller]

Can you regard the sidewalls of the inflated structure as inextensible?