Runge-Kutta Projectile Approximation From Initial Conditions

Click For Summary

Discussion Overview

The discussion revolves around the implementation of the Runge-Kutta method, specifically RK4, for approximating projectile motion in a numerical simulation using Excel. Participants explore how to relate initial conditions to the motion's evolution and compare the accuracy of RK4 with the Euler method.

Discussion Character

  • Exploratory
  • Technical explanation
  • Homework-related

Main Points Raised

  • One participant describes their current simulation using the Euler method and expresses a desire to improve accuracy with RK4.
  • Another participant seeks clarification on how to relate initial conditions to motion evolution using RK4, comparing it to the Euler-Cromer method.
  • There is a question about how to derive the function for the ordinary differential equation (ODE) from given initial conditions.
  • Some participants share resources, including videos and papers, but note that some resources only cover RK2 instead of RK4.
  • One participant defends their choice of using Excel for simulations, citing it as a good starting point for learning scientific programming.

Areas of Agreement / Disagreement

Participants express varying opinions on the appropriateness of using Excel for numerical simulations, with some advocating for programming languages better suited for such tasks. There is no consensus on the best approach to derive the function for the ODE or on the effectiveness of the resources shared.

Contextual Notes

Participants mention limitations in the resources available, particularly regarding the transition from RK2 to RK4, and the need for further clarification on deriving functions from initial conditions.

Who May Find This Useful

This discussion may be useful for individuals interested in numerical methods for physics simulations, particularly those exploring different approximation techniques and their implementations in software like Excel.

VexCarido
Messages
8
Reaction score
4
Hi everyone. I'm a new member, great to be here:)

I have a few questions that I wanted to ask you guys regarding the method by which we implement the Runge-Kutta approximation of Projectile Motion if we should do it using a numerical iterative method with a Spreadsheet like Excel.

I have already constructed a simulation in Excel using the Euler method basic physics formulas and implemented both gravity, drag and wind forces. Now I wish to improve upon the accuracy by using a better approximation of the X,Y coordinates over time with RK4.

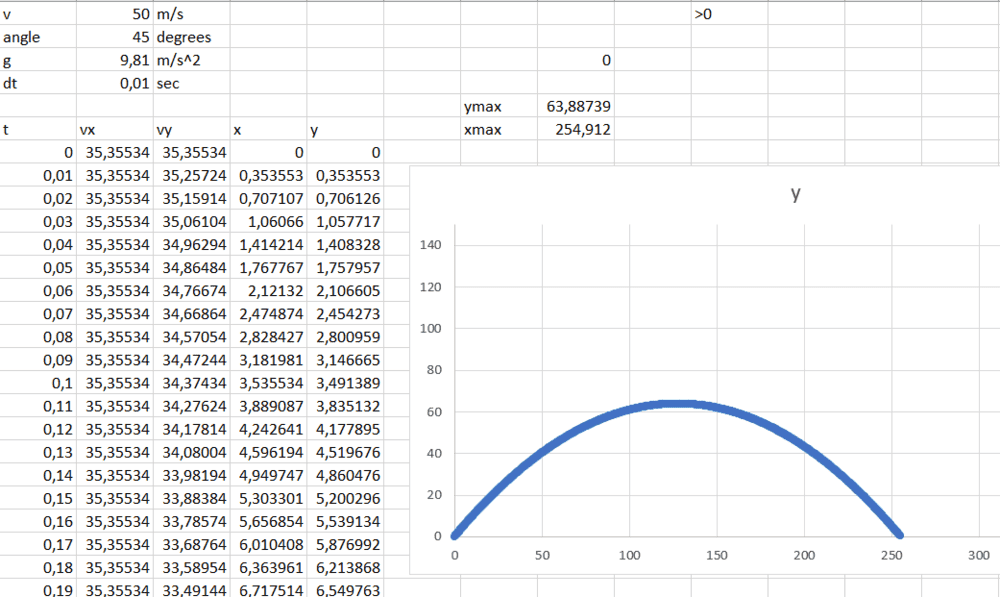
Here's how I constructed the spread sheet with The Euler numerical method (using gravity, but ignoring drag and wind):
70da2c3045fda1b14f8a7a0df03558fe.png


and I suppose these are the formulas that should use to get the improved approximation with the Runge Kutta Method:
Rk4.png
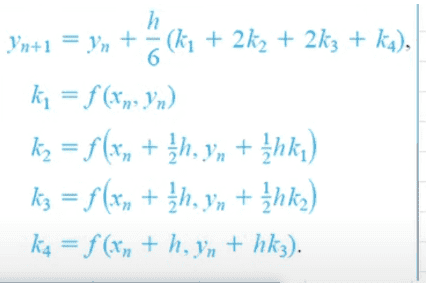To clarify, I am trying to get a list X, Y coordinates as function of time, using a set of initial conditions. The initial values should be able to be freely changed to get approximations of any type of movement along the x-y plane.

I hope my phrasing & terminology is sufficient. This is mostly a DIY project, not homework or school related.
 
Last edited:
Physics news on Phys.org
Hi @VexCarido and welcome to PF.

:welcome:

You said you have a few questions. What are they?
 
kuruman said:
Hi @VexCarido and welcome to PF.

:welcome:

You said you have a few questions. What are they?

I thought it may have been clear from OP, but it may have been too broad. I'm trying to get an understanding of how to relate a set of initial conditions to the evolution of motion, using the RK4 method, in a similar fashion to what you would do with the Euler-Cromer method.

That is, I have an object a x,y position thrusted in any direction with a specified velocity. Using Euler's method I use the simple iteration of x= vx*dt+x, y=vx*dt+y formula.

How can I use the RK4 to solve the exact same problem? I recon I need to calculate the value of the function "f" ? How does one go about it?

My goal is to then compare the two solutions to see how much they diverge over time when I plug in different initial values.
 
Here is a short video that I found with minimal search to get you started. I hope it helps. I am sure there are other examples on the web if it doesn't.
 
kuruman said:
Here is a short video that I found with minimal search to get you started. I hope it helps. I am sure there are other examples on the web if it doesn't.

Unfortunately the video skips a couple of steps in relation to my question and I have looked at other videos that also seem not to mention how I get the function of the ODE from a set of initial conditions.

In this video he uses f=3X^2Y. If I need to go from the information(Example); Starting point (0,0) velocity = 75/ms at (35) degree angle and translate this info into a function, what would be the appropriate steps then?
 
Have you seen this?
 
kuruman said:
Have you seen this?

No, that particular site escaped my search and it does in fact provide some very useful info. Thanks.
Only problem is that it deals with RK2, not 4. Hopefully I will be able to deduce the logic behind it and modify it to suit a forth order approximation instead.
 
Is there any particular reason you are using Excel for this instead of a programming language that is more suited to numerical simulation?
 
VexCarido said:
No, that particular site escaped my search and it does in fact provide some very useful info. Thanks.
Only problem is that it deals with RK2, not 4.

This post might help:
https://scicomp.stackexchange.com/a/21063

This paper compares different methods for ballistics:
https://www.researchgate.net/publication/333985200_Two_Numerical_Algorithms_for_the_Ballistic_Motion_Equations
 
  • #10
boneh3ad said:
Is there any particular reason you are using Excel for this instead of a programming language that is more suited to numerical simulation?

I have been thinking that Excel serves as a very sound starting point for my practice in scientific programming & creating physics simulations. It is very suitable as you are working at a truly fundamental level with all the equations of physics without the need for knowing additional coding languages.

I was inspired by a couple of different persons online who showed me the versatility of the program given a little know-how & I'm confident I'll be able to translate a lot of the knowledge directly to a range of programming languages moving forward.

If you want to see some of the awesome capabilities of Excel (particularly the 2003 version) i suggest you check out this website.: http://www.excelunusual.com/

Or this Youtube Channel (same guy):
 

Similar threads

Undergrad Runge-Kutta 4 w/ some sugar on the top: How to do error approximation?
  • · Replies 65 ·
3
Replies
65
Views
8K
MATLAB Problem with Runge-Kutta script file
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Excel projectile trajectory
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad If we throw a ball with initial velocity v0, is there a force?
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Projectile Intercept Math & Trigonometry
  • · Replies 4 ·
Replies
4
Views
2K
Graduate Runge-Kutta: Maintaining Units in Numerical Methods
  • · Replies 16 ·
Replies
16
Views
4K
Fortran Runge-Kutta using Numerical Recipes
  • · Replies 8 ·
Replies
8
Views
3K
Wrong solution order using Runge Kutta 4
  • · Replies 15 ·
Replies
15
Views
3K
Help with using the Runge-Kutta 4th order method
  • · Replies 14 ·
Replies
14
Views
3K
Undergrad Resolution of a PDE with second order Runge-Kutta
  • · Replies 6 ·
Replies
6
Views
4K