- #1
amjad-sh
- 240
- 13
This thread refers to a paper I am working on.
The paper said in the model section that:
In the complete set of scattering states we distinguish two orthogonal set of eigenfunctions:
(i) the states
− →
ϕ incoming from the left, and (ii) the states
←−
ϕ incoming from the right. Away from the interface the wave functions corresponding to the energy ε = (p^2 +k^2 )/2m have:
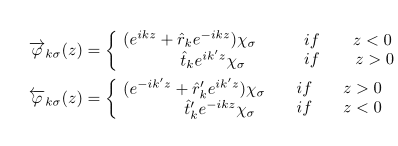My question is : why the wave functions are represented as a combination of plane waves and why in the terms (z<0) for waves incoming from the left and (z>0) for waves coming from the right there is no e^(ik'z) and e^(-ikz) multiplied by nothing?
then the text completes:
Apparently the expressions of Eq. (3) are only valid when k^2>2mV , that is, when the energy of the scattering states is larger then the height of the interface potential barrier. It can be easily proven that the electrons with k^2<2mV do not contribute to the transport effects we are considering in this work.
In general, the matrix scattering coefficients can be represented as follows:
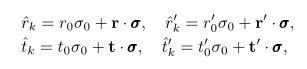
where, ##\sigma_0## is a 2 × 2 unit matrix, and vectors ##\mathbf r,\mathbf r_ 0 ,\mathbf t##,
and ##\mathbf t_0## describe the spin dependent (spin flip) part of the scattering at the interface. A nontrivial spin dependent part of the scattering coefficients, appearing due to the ISOC, is the physical origin of the spin-to-charge and spin-to-spin conversion effects that will be considered in
the next sections.
The text completes:
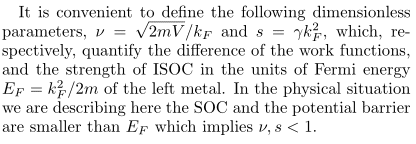
My question: Why the potential barrier is considered smaller than the fermi energy? Is it because we considered the energy of the scattering states bigger than the potential barrier?
@DeathbyGreen Hi sorry I picked you, I wanted to complete the discussion in the previous post https://www.physicsforums.com/threa...rface-between-two-metals.943407/#post-5969726 but I think it may be considered as a new topic.
this is again the paper
The paper said in the model section that:
In the complete set of scattering states we distinguish two orthogonal set of eigenfunctions:
(i) the states
− →
ϕ incoming from the left, and (ii) the states
←−
ϕ incoming from the right. Away from the interface the wave functions corresponding to the energy ε = (p^2 +k^2 )/2m have:
then the text completes:
Apparently the expressions of Eq. (3) are only valid when k^2>2mV , that is, when the energy of the scattering states is larger then the height of the interface potential barrier. It can be easily proven that the electrons with k^2<2mV do not contribute to the transport effects we are considering in this work.
In general, the matrix scattering coefficients can be represented as follows:
where, ##\sigma_0## is a 2 × 2 unit matrix, and vectors ##\mathbf r,\mathbf r_ 0 ,\mathbf t##,
and ##\mathbf t_0## describe the spin dependent (spin flip) part of the scattering at the interface. A nontrivial spin dependent part of the scattering coefficients, appearing due to the ISOC, is the physical origin of the spin-to-charge and spin-to-spin conversion effects that will be considered in
the next sections.
The text completes:
My question: Why the potential barrier is considered smaller than the fermi energy? Is it because we considered the energy of the scattering states bigger than the potential barrier?
@DeathbyGreen Hi sorry I picked you, I wanted to complete the discussion in the previous post https://www.physicsforums.com/threa...rface-between-two-metals.943407/#post-5969726 but I think it may be considered as a new topic.
this is again the paper
