Discussion Overview
The discussion revolves around the classification of a mechanical system as either scleronomic or rheonomic, focusing on the nature of constraints in a system involving pendulums. Participants explore the definitions and characteristics of these types of systems, including the implications of fixed versus time-varying constraints.
Discussion Character
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
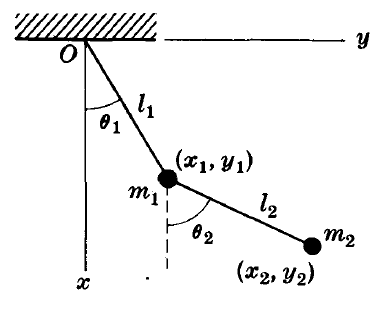
- One participant suggests that the first pendulum represents a scleronomic case due to its fixed constraint, while the second pendulum represents a rheonomic case because its constraint varies with time.
- Another participant questions whether the original inquiry is related to schoolwork.
- A later reply emphasizes the importance of the rod connecting the pendulums as the actual constraint, proposing that the system can be described using constraint equations in Pffafian form, which would indicate a scleronomic system.
- Further clarification is provided that a rheonomic system, such as a rolling disk, involves constraints that relate both positions and velocities of the masses, which cannot be simplified to a position-only relationship.
- There is a caution against confusing rheonomic constraints with nonholonomic constraints, suggesting a nuanced understanding of different types of mechanical constraints is necessary.
Areas of Agreement / Disagreement
Participants express differing views on the classification of the system, with some supporting the idea of a mixed classification and others focusing on specific definitions of scleronomic and rheonomic systems. The discussion remains unresolved regarding the definitive classification of the system in question.
Contextual Notes
Limitations include the potential ambiguity in the definitions of scleronomic and rheonomic systems, as well as the need for clarity on the specific constraints being analyzed. The discussion also highlights the importance of the frame of reference in formulating constraint equations.