Second order inhomogeneous simultaneous differential equations

[TW Cantor]

Homework Statement

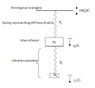
Vibration in a system can be a source of problems. For example, the deck on a ship could vibrate due to the engine which represents a forcing function. This system may be simply modeled by a mass, representing the deck, a spring representing the stiffness of the deck and a forcing function,representing the engine, on the other end of the spring. A vibration absorber is a mechanism which can be attached to the deck in order to absorb the energy in the system by vibrating itself with the deck remaining static. The vibration absorber can be modeled by a mass and spring and these are attached to the first mass spring system, as shown in the diagram. The whole system is modeled by a two spring, two mass system with forcing on one end. This question is concerned with modelling the steady state oscillation of the system.

Let the deck be represented by the mass m1 with stiffness k1 and displacement from equilibrium at time t as x₁(t). Let the vibration absorber be represented by the spring of stiffness k2 and mass m2 with displacement from equilibrium at time t given as x₂(t).

The displacements are given by the second order inhomogeneous simultaneous differential equations:

m₁* (d² x₁ / dt²) = -(k₁+k₂)*x₁ + k₂*x₂ + k₁*sin(p*t)

m₂* (d² x₂ / dt²) = k₂*x₁ - k₂*x₂

where p is the angular frequency of the forcing oscillation.

For, a laboratory model the parameter values are:
m₁ = 0.55
m₂ = 0.16
k₁ = 12.1
k₂ = 1.2

The steady state solutions (ie. solutions after the system has settled down) of the equations of motion will be of the form x₁(t) = a(p)*sin(p*t) and x₂(t) = b(p)*sin(p*t)

Use these two solutions as trial solutions and determine the amplitudes of the displacements a(p) and b(p) by substituting these trial functions into the equations of motion. Note that these amplitudes are functions of p. We are interested in the behaviour of the amplitudes |a(p)| and |b(p)|. Plot these functions in Mathcad and examine the behaviour.

i) Give the amplitude of the deck a(p)
ii) Give the amplitude of the vibration absorber b(p)
iii) There are two forcing frequencies p for which resonance occurs ie. the amplitudes become infinitely big. Give the larger value.
iv) There are two forcing frequencies p for which resonance occurs ie. the amplitudes become infinitely big. Give the smaller value.
v) For what value of p does the vibration absorber absorb all the energy and keep the deck at rest?
vi) What is magnitude of the amplitude |b(p)| of the vibration absorber when it is absorbing all of the energy?

The Attempt at a Solution

i have managed to answer parts i, ii, and v for this question but am unsure as to how calculate the rest.
i) a(p) = (12.1*(1.2 - 0.16*p²))/((13.3 - 0.55*p²)*(1.2 - 0.16*p²) - 1.44)

ii) b(p) = 14.52 / ((13.3 - 0.55*p²)*(1.2 - 0.16*p²) - 1.44)

and for part v:
(12.1*(1.2 - 0.16*p²)) = 0
therefore p=2.7386

if anyone can give me any clues about how to go about solving the other parts of the question i would really appreciate it :-)

 

[lanedance]

for iii) and iv) when do the coefficients become undefined? think about the denominators, and p, the forcing frequency

 

[lanedance]

if you have answered v, substitute the value of p you found into b(p)

 

[TW Cantor]

ok i have got the answer for part vi now, thanks lanedance :-)

for parts iii and iv, would it be when the denominator is equal to zero?

 

[TW Cantor]

yes it is, i was trying that before but my answers kept coming up different to those given. i must have made some mistake when i rearranged the denominator. thanks for your tips :-)