Seeking Guidance to Find Surface & Volume Bound Charges of a Half Cone

[warhammer]

Homework Statement

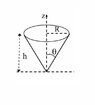
Cone shown in figure has half angle θ, vertical height h & radius R. Its axis is along z direction. Cone is polarised along z direction with Vector P= P(o)z(zhat) where P(o) is a constant. Find surface & volume bound charge density.

Relevant Equations

σ(b)= P(vector) * (nhat)
ρ(b)= - ∇* P(vector)

This was a trivial question I had (which I posted here on the PF EM Forum: https://www.physicsforums.com/threads/bound-charges-polarisation-of-a-half-cone.1015308/).

As I received no response on the above link I decided to post the same as a self formulated HW problem. Below I have attached an image of the cone as well as my solution in chronological order.

I request someone to please have a look and guide me if my approach to find the Surface & Volume Bound Charges is fine or not. If it isn't, I would also request guidance on how to find it correctly.

 

[TSny]

For $\sigma_b$ at a point on the lateral side (sloping surface) of the cone, I follow you up to where you get $\sigma_b = -r \sin\theta \cos\theta$. Here, $r$ is the distance from the point of interest to the vertex of the cone. Note that $\sigma_b$ varies with $r$, so it is not a constant on the lateral side. But then you went on to write this in terms of the total height $h$ of the cone and the radius $R$ of the cone: $\sigma_b= -\frac{P_0 h R}{\sqrt{R^2+h^2}}$. The right-hand side is now a constant, which you know is not the case.

If you want, you can express $\sigma_b$ for the lateral side in terms of $z$ instead of $r$. You found $\sigma_b = P_0z (\hat z \cdot \hat n)$. Express $\hat z \cdot \hat n$ in terms of $\theta$.

For finding the volume charge density, try using Cartesian coordinates for calculating the divergence. I think you'll see that it is much easier than using spherical coordinates.

What about the surface charge density on the top circular surface of the cone?

 

[warhammer]

For $\sigma_b$ at a point on the lateral side (sloping surface) of the cone, I follow you up to where you get $\sigma_b = -r \sin\theta \cos\theta$. Here, $r$ is the distance from the point of interest to the vertex of the cone. Note that $\sigma_b$ varies with $r$, so it is not a constant on the lateral side. But then you went on to write this in terms of the total height $h$ of the cone and the radius $R$ of the cone: $\sigma_b= -\frac{P_0 h R}{\sqrt{R^2+h^2}}$. The right-hand side is now a constant, which you know is not the case.

If you want, you can express $\sigma_b$ for the lateral side in terms of $z$ instead of $r$. You found $\sigma_b = P_0z (\hat z \cdot \hat n)$. Express $\hat z \cdot \hat n$ in terms of $\theta$.

For finding the volume charge density, try using Cartesian coordinates for calculating the divergence. I think you'll see that it is much easier than using spherical coordinates.

What about the surface charge density on the top circular surface of the cone?

Thank you so much sir for your prompt response. For the lateral side keeping in mind I cannot use constants, the value of $\sigma_b=-P_0r\sin\theta\cos\theta$ . I hope this is now the correct representation..

Yes! I mistakenly went through the flow and calculated volume charge density in SPC when it is much simpler and easier to use the Cartesian Coordinates here.

I was having trouble while trying to focus on surface charge density at the circular surface.. I was not able to visualise how and what coordinates will be altered or if it will altogether factor in or not.. Would you please offer some guidance on how to proceed with the same

 

[TSny]

Your expression for $\sigma_b$ for the lateral side looks good.

For the top surface, you can use your formula $\sigma_b = P_0 z( \hat z \cdot \hat n)$ with appropriate values of $z$ and $\hat z \cdot \hat n$.

 

[berkeman]

Thread is closed temporarily for Moderation...

 

[berkeman]

Thread will remain closed by the request of the OP. He has found that his approach to this problem was wrong, and does not want to proceed further along these lines. Thank you very much to @TSny for your help on this.