Fabio010
- 84
- 0
Semicircular Wire
A positively charged wire is bent into a semicircle of radius R, as shown in Figure 2.15.4.
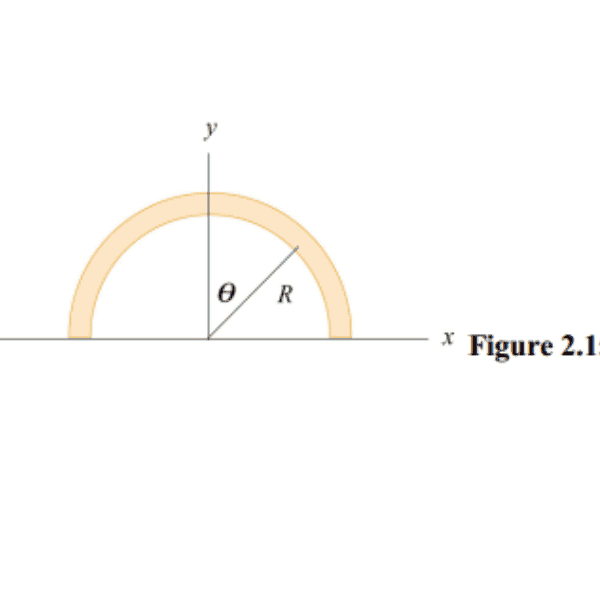
The total charge on the semicircle is Q. However, the charge per unit length along the
semicircle is non-uniform and given by
λ = λo θ cos .
(a) What is the relationship betweenλo , R and Q?
(b) If a charge q is placed at the origin, what is the total force on the charge?
Attempts:
a)
dq = λdl = λRdθ
dq = λo.cosθ.R.dθ
Q = ∫(-pi/2 to pi/2) [λo.cosθ.R.dθ]
Q = 2λoR
b)
Force in x-axis = ((Ke.q.λo.cosθ.R.dθ)/(R^2))*sinθ integrating that in order to dθ, the result is zero.
Force in y-axis = ((Ke.q.λo.cosθ.R.dθ)/(R^2))*cosθ integrating that in order to dθ, the result is (Ke.q.λo/R)*(0.5*pi)
Is that correct??
A positively charged wire is bent into a semicircle of radius R, as shown in Figure 2.15.4.
The total charge on the semicircle is Q. However, the charge per unit length along the
semicircle is non-uniform and given by
λ = λo θ cos .
(a) What is the relationship betweenλo , R and Q?
(b) If a charge q is placed at the origin, what is the total force on the charge?
Attempts:
a)
dq = λdl = λRdθ
dq = λo.cosθ.R.dθ
Q = ∫(-pi/2 to pi/2) [λo.cosθ.R.dθ]
Q = 2λoR
b)
Force in x-axis = ((Ke.q.λo.cosθ.R.dθ)/(R^2))*sinθ integrating that in order to dθ, the result is zero.
Force in y-axis = ((Ke.q.λo.cosθ.R.dθ)/(R^2))*cosθ integrating that in order to dθ, the result is (Ke.q.λo/R)*(0.5*pi)
Is that correct??
Last edited: