berlinspeed
- 26
- 4
- TL;DR
- The use of semicolon notation as covariant derivative
Can someone clarify the use of semicolon in
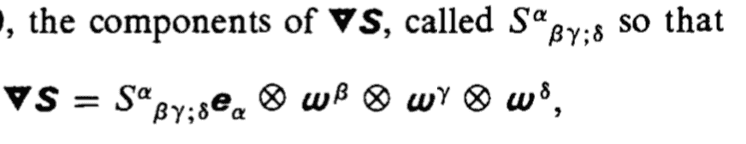
I know that semicolon can mean covariant derivative, here is it being used in the same way (is
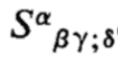 expandable?) Or is
expandable?) Or is
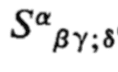 a compact notation solely for the components of
a compact notation solely for the components of
 ?
?
I know that semicolon can mean covariant derivative, here is it being used in the same way (is