Semiconductor and fermi energy

[iScience]

hey guys i just wanted to confirm something;

so, for systems of continuous energy states (or small separations of discrete energy states), we can plot a graph like this and call the fermi energy the middle point where Probability=1/2. like this

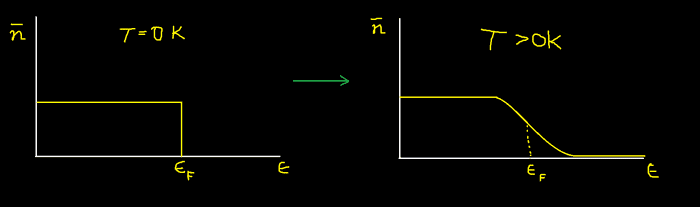
where, if T=0K, the transition from occupancy to no occupancy is sharp. as T increases the fermi level doesn't change, as the constituent particles say... the electrons, occupy higher energy states. but this is for a smooth ("smooth"...) distribution of energy states.

but for the case of a semiconductor, where the existent energy states are not so smooth going from the valence band to the conduction band, how do i know where the fermi energy level is?

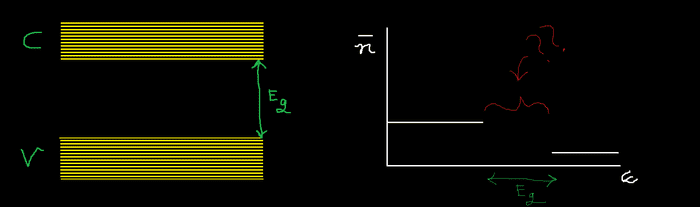
the graph in this image/scenario I've plotted for a non-zero temperature case (as apparent by the nonzero occupancy in the C-band region).
Take a look at the red region; I'm almost sure that this region should have zero occupancy of electrons BUT, I'm reading an introductory paper on semiconductors and they are referring to the fermi level being right in the middle between the V-band and C-band for the case where there are no excess carriers (no excess electrons and no excess holes).
I don't understand how the fermi level can be in the middle when the fermi level is defined as (i thought..) the energy at which the probability of occupancy is 1/2. but the occupancy probability in the band gap is zero.. so how can it be there?

thanks

 

[mfb]

If there are no states available, the Fermi level is the energy where (hypothetical) states would be filled to 50%.

as T increases the fermi level doesn't change

In general it does change a bit, but that is unrelated to the main question.

 

[iScience]

In general it does change a bit, but that is unrelated to the main question.

i thought the electrons at the edges entering the higher energy states corresponds to the curve just becoming smoother with the 50% point remaining the same. Could you give me a brief explanation of what is changing the fermi level?

If there are no states available, the Fermi level is the energy where (hypothetical) states would be filled to 50%.

so then am i just drawing a smooth hypothetical curve from the valence band energy edge to the conduction band energy edge and then calling the fermi level where the y-axis (\bar{n}) hits 1/2?

 

[mfb]

i thought the electrons at the edges entering the higher energy states corresponds to the curve just becoming smoother with the 50% point remaining the same. Could you give me a brief explanation of what is changing the fermi level?

The curve is not perfectly symmetric. This is obvious where you reach the lowest energy states (as there are no electrons below 0, but electrons can be above 2*E_f), but the asymmetry exists everywhere. For small temperatures this is a small effect.

so then am i just drawing a smooth hypothetical curve from the valence band energy edge to the conduction band energy edge and then calling the fermi level where the y-axis (\bar{n}) hits 1/2?

Right.