- #1
Spinnor
Gold Member
- 2,216
- 430
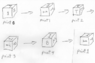
I am trying to understand the picture below which is of a contractible and uncontractible loop in what I would call (proper name?) "rotation space", where "rotation space" is a solid ball of radius π with opposite points on the surface of the ball identified, each point of the ball representing a direction and angle less than or equal to π which could represent the rotation of an object. I understand what a point represents in such a space but I am having a hard time understanding what a path in such a space represents, for example the two paths below. I am thinking that the path represents some kind of "rotation history" of an object but something does not seem right about that idea. I know the answer must be simple but I am stuck.

The above was found at, http://www.damtp.cam.ac.uk/user/examples/D18S.pdf
(which Google Chrome tells me is not secure)
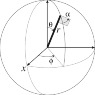
I think my second question is related so I ask it here. I would like to represent the rotational history of an object, say a soccer ball. Let the soccer ball have a spherical coordinate system printed on it. Say the ball is rotating relative to say a soccer field, we will(?) need 6 (edit, 7) coordinates to describe the rotational history of the ball, 2 spherical coordinates give the orientation of the ball with respect the the soccer field, (edit, another angle is needed to to fix the orientation), 2 more coordinates give the orientation of the instantaneous angular momentum vector L of the soccer ball, another coordinate gives the magnitude of L and one more coordinate for time. Is 6 (edit, 7) the minimum number of coordinates to describe the rotational history of the ball or are some of my coordinates redundant? Is such a space the same as S^2xS^2xR^2 (edit, S^2xS^3xR^2) ?
Edit, I should not post questions at the end of the day. If we know the orientation of the soccer ball as a function of time, 3 coordinates plus time, we know the rotational history of the soccer ball, right?
Edit, sorry for mistakes.
Thanks for any help.
The above was found at, http://www.damtp.cam.ac.uk/user/examples/D18S.pdf
(which Google Chrome tells me is not secure)
I think my second question is related so I ask it here. I would like to represent the rotational history of an object, say a soccer ball. Let the soccer ball have a spherical coordinate system printed on it. Say the ball is rotating relative to say a soccer field, we will(?) need 6 (edit, 7) coordinates to describe the rotational history of the ball, 2 spherical coordinates give the orientation of the ball with respect the the soccer field, (edit, another angle is needed to to fix the orientation), 2 more coordinates give the orientation of the instantaneous angular momentum vector L of the soccer ball, another coordinate gives the magnitude of L and one more coordinate for time. Is 6 (edit, 7) the minimum number of coordinates to describe the rotational history of the ball or are some of my coordinates redundant? Is such a space the same as S^2xS^2xR^2 (edit, S^2xS^3xR^2) ?
Edit, I should not post questions at the end of the day. If we know the orientation of the soccer ball as a function of time, 3 coordinates plus time, we know the rotational history of the soccer ball, right?
Edit, sorry for mistakes.
Thanks for any help.
Attachments
Last edited: