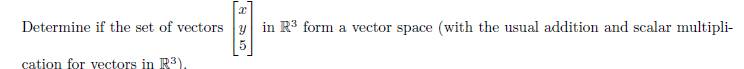Set of vectors form a vector space

[karush]

View attachment 8769this is what is given
so by addition
$$\begin{bmatrix}x_1\\y_1\\5z_1\end{bmatrix}
\oplus
\begin{bmatrix} x_2\\y_2\\5z_2
\end{bmatrix}
=
\begin{bmatrix}
x_1+x_2\\y_1+y_2\\5z_1+5z_2
\end{bmatrix}
=
\begin{bmatrix}
X\\Y\\10Z
\end{bmatrix}$$

uhmmmm really?

 

[topsquark]

this is what is given
so by addition
$$\begin{bmatrix}x_1\\y_1\\5z_1\end{bmatrix}
\oplus
\begin{bmatrix} x_2\\y_2\\5z_2
\end{bmatrix}
=
\begin{bmatrix}
x_1+x_2\\y_1+y_2\\5z_1+5z_2
\end{bmatrix}
=
\begin{bmatrix}
X\\Y\\10Z
\end{bmatrix}$$

uhmmmm really?

This time there are no z's. Or z = 5 in all cases, if you prefer to look at it that way.
[math]\left [ \begin{matrix} x_1 \\ y_1 \\ 5 \end{matrix} \right ] \oplus \left [ \begin{matrix} x_2 \\ y_2 \\ 5 \end{matrix} \right ] = \left [ \begin{matrix} x_1 + x_2 \\ y_1 + y_2 \\ 5 + 5 \end{matrix} \right ] \notin \left [ \begin{matrix} X \\ Y \\ 5 \end{matrix} \right ] [/math]

so addition is not closed this time.

-Dan

 

[karush]

https://dl.orangedox.com/GXEVNm73NxaGC9F7Cy