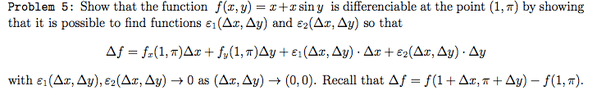SUMMARY
This discussion focuses on demonstrating the differentiability of the function f(x,y) through a specific equation involving Δx and Δy. The equation to prove is (1+Δx) + (1+Δx)sin(pi+Δy) - 1 = Δx - Δy + ε(Δx,Δy)Δx + ε(Δx,Δy)Δy. Key transformations include recognizing that sin(pi+Δy) simplifies to -sin(Δy), leading to the expression Δx - sin(Δy) - Δxsin(Δy). The discussion emphasizes the need to define ε(Δx,Δy) functions that converge to zero as (Δx,Δy) approaches (0,0).
PREREQUISITES
- Understanding of multivariable calculus, specifically differentiability.
- Familiarity with Taylor series expansions and limits.
- Knowledge of trigonometric identities, particularly sin(π + y).
- Proficiency in mathematical notation and epsilon-delta definitions.
NEXT STEPS
- Study the concept of differentiability in multivariable functions.
- Learn about the epsilon-delta definition of limits in calculus.
- Explore Taylor series expansions for functions of multiple variables.
- Investigate trigonometric identities and their applications in calculus.
USEFUL FOR
Students and educators in mathematics, particularly those studying calculus and analysis, as well as anyone involved in proving properties of multivariable functions.