Showing that a multivariable limit does not exist

[ek124]

TL;DR

how to show a multivariable limit does not exist/exist

I want to show that the limit of the following exists or does not exist:

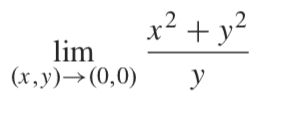
When going along the path x=0 the limit will tend to 0 thus if the limit exists it will be approaching the value 0
when going along the path y=0, we get an equation with divisibility by zero. Since this is not possible does this already show that the limit does not exist? Or does it simply mean that there is an asymptote... I would like to know what this means.
Finally when going along the path y=x^2, the limit tends to 1. Since the first and last path give a different outcome the limit DNE however I want to know what the path along y=0 tells us anyway.

 

[ek124]

nvm it's solved

 

[BvU]

i.e. does not exist ?

 

[Abdullah Almosalami]

I want to know what the path along y=0 tells us anyway.

I was going to say if you rewrite the function inside the limit as $\frac {x^2} {y} + y$, then perhaps that offers a better perspective but I'm not sure.

I think actually seeing that the top has $x^2 + y^2$, that should immediately strike you as saying that changing the function into its polar equivalent might be helpful for the limit. We know that $x^2 + y^2 = r^2$ and $y = r * \sin\theta$, and the limit along the line $y = 0$ corresponds to $\theta = 0$ from the right side and $\theta = \pi$ from the left, hence we have:

$\lim_{(r, \theta) \rightarrow (0,0)} {\frac {r^2} {r*\sin\theta}} = \lim_{(r, \theta) \rightarrow (0,0)} {\frac {r} {\sin\theta}}$

Yeah this seems to lead to the same undefined issue as well.

Even thinking about this numerically leads to the same issues.

So I think if a function is undefined for that entire line of $y=0$, then we cannot really use the idea of a limit here. I could be wrong, but that's what I got for now.