Showing that these two integrals are equal

[conv]

Homework Statement:

Integrals

Relevant Equations:

Written down below

Mentor note: The OP has been notified that more of an effort must be shown in future posts.
These two are equal to each other, but I can't figure out how they can be that.

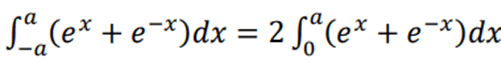
I know that 2 can be taken out if its in the function, but where does the 2 come from here?

 

[PeroK]

Why not evaluate the integrals to check they are the same?

If you do that you might see for yourself where the $2$ comes from.

 

[conv]

so do i solve for the integral on the left side and end up with the integral on the right?? Or do i solve them just as they are written above?


(I have solved the equation with values, but don't really know how to do this one. )

 

[PeroK]

so do i solve for the integral on the left side and end up with the integral on the right?? Or do i solve them just as they are written above?


(I have solved the equation with values, but don't really know how to do this one. )

I suggest you evaluate both integrals. And check they are equal.

I assume you know how to integrate $e^x$ and $e^{-x}$?

 

[conv]

i understood it. Thanks

 

i understood it. Thanks

More generally, if $f(x) = f(-x)$ then $\int_{-a}^a f(x) = 2\int_0^a f(x)$. On the other hand, if $f(x) = -f(-x)$ then $\int_{-a}^a f(x) = 0$. Can you see why $f(x) = e^x + e^{-x}$ satisfies $f(x) = f(-x)$?

 

[epenguin]

This should be almost self-evident and not difficult to argue from the symmetry around 0 between the two functions $e^x$ and $e^{-x}$. If in doubt about that, plot them. Which would only be reminding yourself of what you should securely know already. Not clever but rather basic.

ETA OK this is equivalent to what etotheipi says.