Two ways of integration giving different results

[Valour549]

Homework Statement

Please see below

Relevant Equations

Please see below

I am trying to do the double integral.

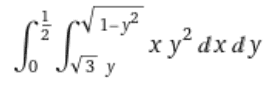
And I remembered there's this formula that says if the integrand can be split into products of F(x) and G(y) then we can do each one separately, then take the product of each result. Taken from Stewart's Calculus 9E.

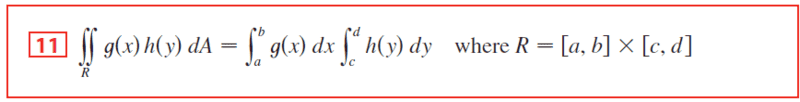
So I tried to do the integral two ways, the first is splitting them and the second not.

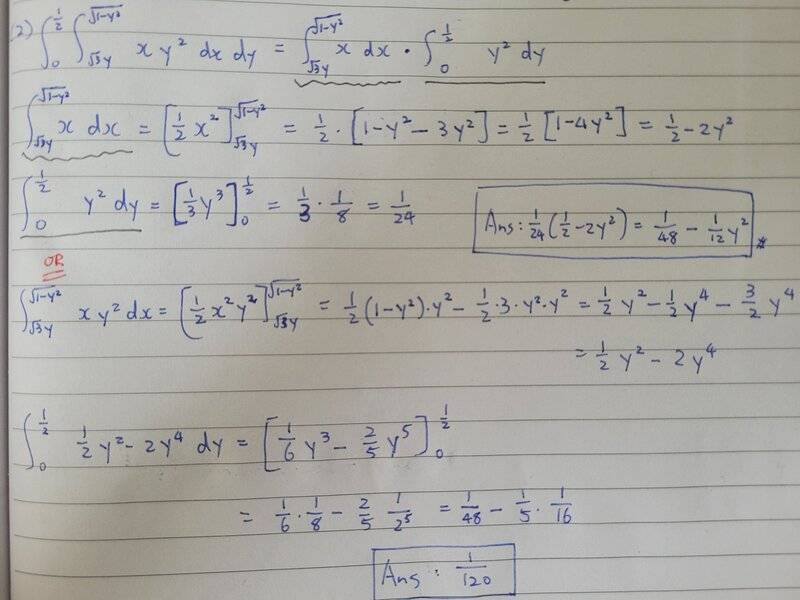
I'm fairly sure the correct answer is the second one. So is the right conclusion that formula above doesn't work when the limits of integration are variables, and only work when the limits of integration are pure numbers? Stewart does not caution this, and I myself cannot figure out why the formula suddenly doesn't work when the limits of integration are variables.

 

[hutchphd]

The issue is not that the limits contain "variables" per se but that you are integrating over that variable (y in this case). You simply cannot do the first step in your facsimile.

 

[Valour549]

Let me see if I got this right: if any of the limits of integration contains a variable, then it cannot be separated from the integrand which integrates wrt that variable?

 

[hutchphd]

I believe you need to not memorize a "rule" but understand what you are doing. If I have an integral of the form $$\int f(y) g(y) dy$$ where f and g are arbitrary functions I cannot somehow say $$\int f(y) g(y) dy=g(y)\int f(y) dy~~~~~(no,no,no)$$ Your mistake iis very fundamental. The integral over x produces a function of y, not a number.

 

[PeroK]

Let me see if I got this right: if any of the limits of integration contains a variable, then it cannot be separated from the integrand which integrates wrt that variable?

The way I would explain it is this. If you integrate with respect to $x$ you may have $y$ in the bounds. If you integrate with respect to $y$ you cannot have the same variable $y$ also in the bounds. In other words, it makes no sense to have the endpoints defined in terms of the variable with which you are integrating.

It's like having $\sum_{n =1}^n n^2$. Try to write out what that could possibly mean.

 

[Valour549]

The way I would explain it is this. If you integrate with respect to $x$ you may have $y$ in the bounds. If you integrate with respect to $y$ you cannot have the same variable $y$ also in the bounds. In other words, it makes no sense to have the endpoints defined in terms of the variable with which you are integrating.

It's like having $\sum_{n =1}^n n^2$. Try to write out what that could possibly mean.

Yes I was aware of the fact you mention regarding the that we cannot integrate wrt to x and also have x in the limits of integration.

So what about the rule Stewart wrote (the one boxed in red), does that only apply when the limits of integration are actual numbers? Or anytime when the limits of integration doesn't contain the variable we are integrating wrt?

 

[PeroK]

Yes I was aware of the fact you mention regarding the that we cannot integrate wrt to x and also have x in the limits of integration.

So what about the rule Stewart wrote (the one boxed in red), does that only apply when the limits of integration are actual numbers? Or anytime when the limits of integration doesn't contain the variable we are integrating wrt?

As far as I can tell Stewart is only presenting the simplest case where the region over which you are integrating is a rectangle.

 

[FactChecker]

In the limits on the $x$ integral on the right side of the first line, what is the value of $y$?
$\int_{\sqrt{3}y}^{\sqrt{1-y^2}} x \,dx$
It should be running through the range of values in the integral wrt y.

 

[Mark44]

As far as I can tell Stewart is only presenting the simplest case where the region over which you are integrating is a rectangle.

Yes, the region is a rectangle. In the photo it defines R as $[a, b] \times [c, d]$.

 

[vela]

And I remembered there's this formula that says if the integrand can be split into products of F(x) and G(y) then we can do each one separately, then take the product of each result. Taken from Stewart's Calculus 9E.

That's not exactly what Stewart says. He says if the integrand can be split into a product of F(x) and G(y) and you are integrating over the rectangle $[a,b]\times[c,d]$, then the original integral is equal to the product of the individual integrals. In the example you gave, the region over which you are integrating isn't a rectangle, so the rule you cited doesn't apply.

Say F'(x) = f(x), then you have
$$\int_{p(y)}^{q(y)} f(x)\,dx = F(x)\bigg|_{p(y)}^{q(y)} = F(q(y))-F(p(y)),$$ which is clearly a function of $y$, so you can't pull it out of the integral wrt $y$. If the limits don't depend on $y$, then you have
$$\int_a^b f(x)\,dx = F(b)-F(a) = \text{constant}.$$ Since the result is a constant, you can pull it out of the integral wrt $y$ (just like you can with any other constant). That's why the rule Stewart gave works.