Silicon FCC -- Why are so many atoms shown in the lattice?

[pj33]

TL;DR

Explanation of lattice

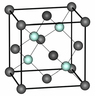
https://www.researchgate.net/figure/1-Silicon-crystallographic-structure-It-has-the-diamond-structure-which-is-two-fcc_fig4_34172659 the fcc silicon lattice is shown.
My question is:
Since the silicon atom has 4 valence electrons and requires 4 more to be completed, why are so many atoms shown in the lattice. There are 8 electrons shown as nodes and each of it, is connected to a neighbouring node, thus each silison requires one more to be complete.
Also, what is the difference between the blue-ish and grey atoms?
Sorry for this silly question, but I didnt study chemistry extensively in the past and I find some concepts hard to understand.

Thank you in advance

 

[Borek]

It is not about a compound (in which case electrons/bonds would matter), it is about a lattice - so it has to show the smallest repeatable cell. Note that each atom is connected to four other (just like you expected).

Also: I am not sure what you mean by "electrons shown as nodes".

Blue atoms are those completely inside the cell, grey ones are on the walls and they are shared with neighboring cells, they don't count as whole when counting cell atoms.

 

[DrDu]

The cell shown is not a minimal cell, which would contain only two atoms, one black and the other blue. The black and blue positions cannot be mapped upon each other by a simple shift of the whole lattice, therefore, they are inequivalent. Each Si has 4 covalent bonds to 4 neighbouring atoms.

 

[pj33]

It is not about a compound (in which case electrons/bonds would matter), it is about a lattice - so it has to show the smallest repeatable cell. Note that each atom is connected to four other (just like you expected).

Also: I am not sure what you mean by "electrons shown as nodes".

Blue atoms are those completely inside the cell, grey ones are on the walls and they are shared with neighboring cells, they don't count as whole when counting cell atoms.

I see, I got it wrong, by "electrons shwon as nodes" I meant the spheres that form the cube, so those are the Si atoms.

 

[pj33]

The cell shown is not a minimal cell, which would contain only two atoms, one black and the other blue. The black and blue positions cannot be mapped upon each other by a simple shift of the whole lattice, therefore, they are inequivalent. Each Si has 4 covalent bonds to 4 neighbouring atoms.

Can you explain this in a bit more detail please.
I though this correspond to the configuration of the minimum number of atoms thus all of the to have a complete outer layer.
Correct me if I am wrong, but since the Si atom has 4valence electrons and it needs 4 more to be complete, doesn't this mean that it needs at least 4 more atoms thus the most efficient shape possible is the one shown above. Can 2 Si atoms be suffiecient by sharing 8 electrons simultaneously?
If this is true, then what does the above shape mean/ porpuse?

 

[DrDu]

The number of atoms in a cell is not directly related to the number of bonds, as bonds may exist between atoms in different cells.