Simple Equivalence Problem- help please (First Year Statics)

[lc99]

<< Mentor Note -- Thread moved from the technical forums, so no Homework Template is shown >>

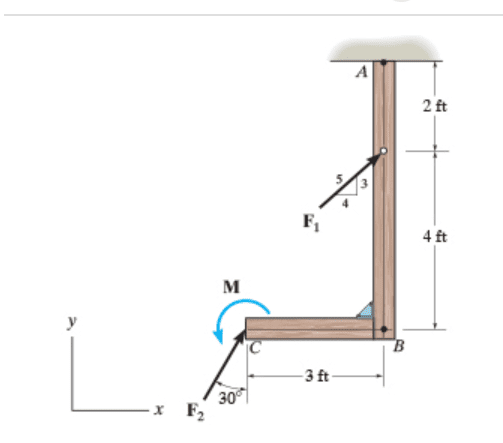
Okay, so i am having severe problems with figuring out what i did wrong...
I am given : F1 = 250 and F2 = 90
The correct Force result is = 245 i +228 j with magnitude of 335 .
The moment given is 500 lb*ft.

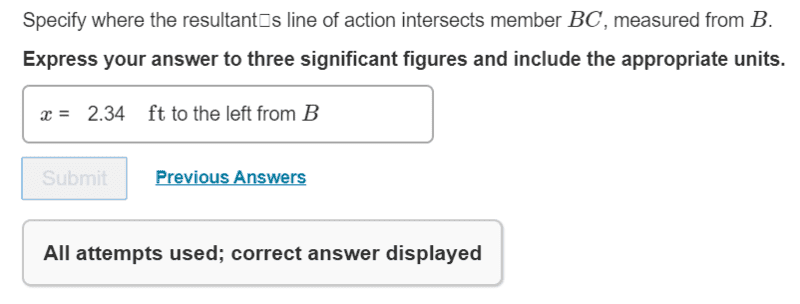
I am trying to find the result's line of action that would intersect member BC measured from B. The correct answer is x = 2.34.

But, i got some other answer. I found the location of intersection with M = Fy * x (Fy because Fx would be 0 along the x-axis).

so , 500 = 228*x --> x = 2.19?? Which is wrong :(

 

[haruspex]

The correct Force result is = 245 i +228 j with magnitude of 335 .

Ok, but that also has, of itself, a line of action. It would pass through the point of intersection of the lines of action of F1 and F2. You have not factored this in.
The safer approach is to pick an axis and find the sum of miments about it from the applied forces. Then find the line of action of the resuktant that yields the same moment.

 

[lc99]

Ok, but that also has, of itself, a line of action. It would pass through the point of intersection of the lines of action of F1 and F2. You have not factored this in.
The safer approach is to pick an axis and find the sum of miments about it from the applied forces. Then find the line of action of the resuktant that yields the same moment.

Thanks! I figured out that i didn't add up all the moments