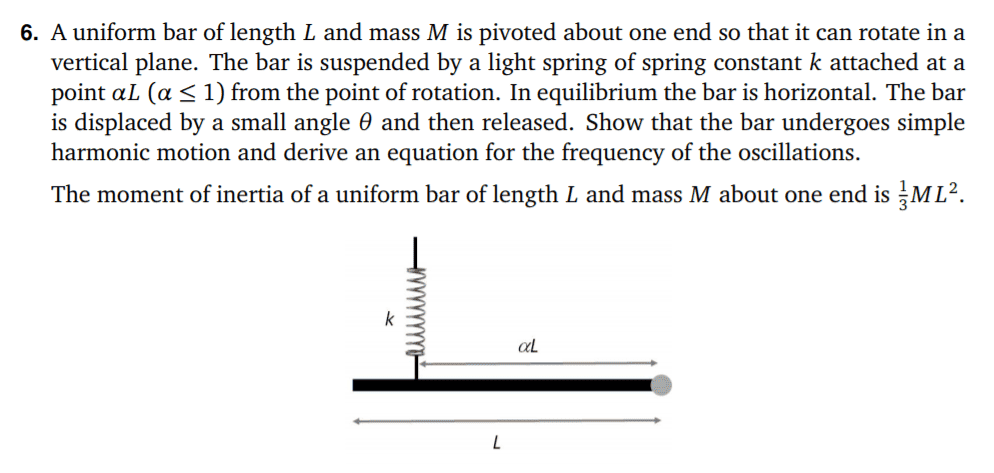
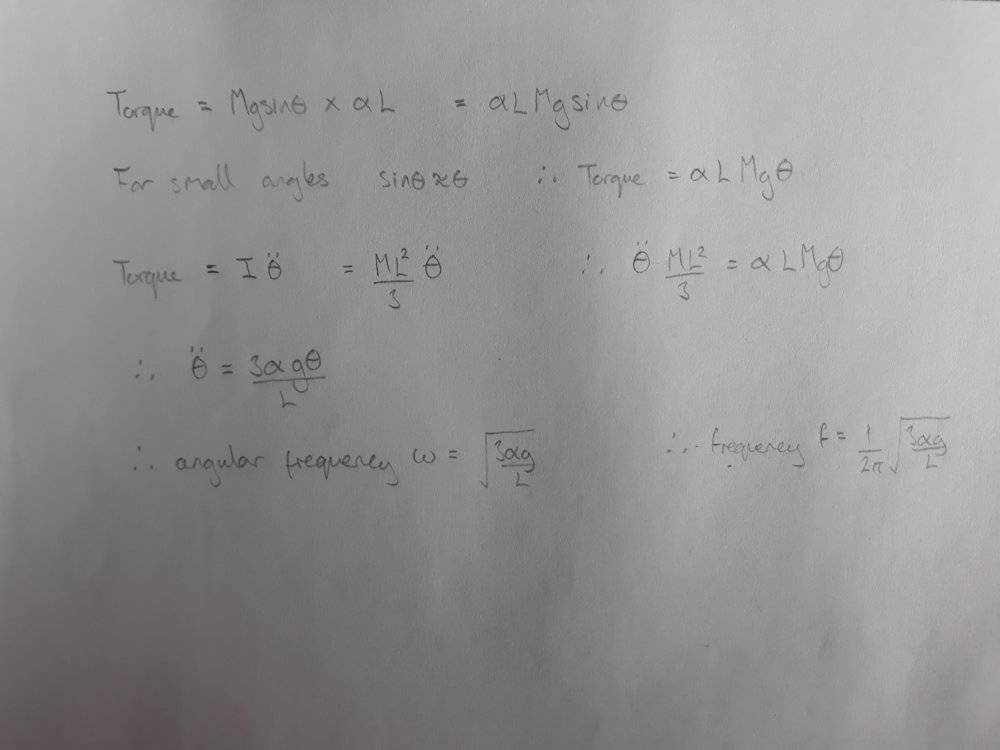SUMMARY
The discussion focuses on calculating the frequency of oscillations for a bar pivoted at one end, influenced by a spring. The professor's formula for frequency is $$f=\frac{1}{2\pi}\sqrt{\frac{3\alpha^2k}{M}}$$, where ##k## represents the spring constant and ##M## is the mass of the bar. Participants highlight the importance of torque calculations, specifically the relationship between gravitational force and spring force, and the need to express the restoring torque in terms of angular displacement ##\theta##. The conversation emphasizes the necessity of understanding equilibrium conditions and the forces acting on the bar.
PREREQUISITES
- Understanding of simple harmonic motion principles
- Familiarity with torque and angular displacement concepts
- Knowledge of spring constants and their role in oscillatory systems
- Basic grasp of equilibrium conditions in mechanical systems
NEXT STEPS
- Study the derivation of the frequency formula for oscillating systems involving springs
- Learn about torque calculations in rotational dynamics
- Explore the effects of spring constants on oscillation frequency
- Investigate equilibrium conditions for systems involving multiple forces
USEFUL FOR
Students of physics, mechanical engineers, and anyone interested in the dynamics of oscillating systems involving springs and rigid bodies.