Simple Harmonic Oscillator with Boundary Conditions

[blizzardof96]

How would you solve for the Amplitude(A) and Phase Constant(ø) of a spring undergoing simple harmonic motion given the following boundary conditions:

(x1,t1)=(0.01, 0)
(x2,t2)=(0.04, 5)
f=13Hz

x values are given in relation to the equilibrium point.

Equation of Motion for a spring undergoing SHM

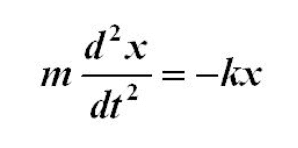Solution to the 2nd order ODE

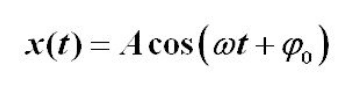
Any hints or help would be much appreciated.

 

[anorlunda]

Our rules say that you must show your attempt at a solution before we are allowed to help you. Show us your work.

 

[blizzardof96]

Attempt at a solution
x(t1)=Acos(wt1+ø)

Therefore:
(1) 0.01=Acos(ø)

x(t2)=Acos(wt2+ø)

(2) 0.04=Acos(5w+ø)

w=2pif
w=2pi(13)=81.69

(2) becomes 0.04=Acos(408.4+ø)

This leaves us with the following equations to be solved for A and ø. This is where I am struggling.
(1) 0.01=Acos(ø)
(2) 0.04=Acos(408.4+ø)

 

[kuruman]

One way to proceed is to divide the second equation by the first to eliminate A. What do you get? Remember the identities $\cos(a+b) = \cos a*\cos b - \sin a*\sin b$ and $\sin x = \sqrt{1-\cos^2x}.$

 

[Arman777]

Maybe we shouldn't approach just by using the giving equation. Equation 2 in the OP post but deducing the formule from the start. Finding constants in x(t) equation and then proceed. How this sounds ?

 

[kuruman]

Maybe we shouldn't approach just by using the giving equation. Equation 2 in the OP post but deducing the formule from the start. Finding constants in x(t) equation and then proceed. How this sounds ?

Isn't this what OP is doing by writing down equations (1) and (2)? It's a system of two equations and two unknowns that OP is wondering how to solve.

 

[Arman777]

Isn't this what OP is doing by writing down equations (1) and (2)? It's a system of two equations and two unknowns that OP is wondering how to solve.

I am confused about something and it might be helpful to the OP.

Now we have a second order diff eqn and 2 boundry conditions. So we can see that the solution will have a form of
$$ x(t) =c_1sin(\sqrt (\frac {k} {m})t)+c_2cos(\sqrt (\frac {k} {m})t)$$ (Eq.1)

Since its a boundry condition I derived the conditon from $$m(d^2x/dt^2) + kx = 0$$ then I said, $$(d^2x/dt^2) + (k/m)x = 0$$ where λ=k/m and then we get the above equation.

Now we have 2 boundry conditions so I thought we should put those into the Eq.1 and then try to find c1 and c2. when we do that it seems that they are not both zero. So after that we need to do some calculations to turn it into the like the $cos(a+b)$ thing as you said.
$$x(t) = Acos(ωt+Φ)$$

 

[blizzardof96]

The cos(a+b) identity was helpful. This is how I solved for ø and A.

x(t)=Acos(ωt+ø)

(1) 0.01=Acos(ø)
(2) 0.04=Acos(ωt+ø) where ωt is some constant k
(3) 0.04=Acos(k+ø)

(3)/(1)
4=cos(k+ø)/cos(ø)

using the identify cos(a+b)=cosa∗cosb−sina∗sinb we can proceed.

(4) 4cos(ø)=cos(k)*cos(ø)-sin(k)*sin(ø)

dividing through by cos(ø)

(5) 4=cos(k)-sin(k)*tan(ø)

(6) Arctan(cos(k)-4)/sin(k))=ø

ø= -77.36 degrees

Subbing back into original equations we get an ampitude(A) of 0.046.

 

[kuruman]

Did you check your work? Do you get a displacement of 0.04 when you put your values for A and φ back in the original equation? Your method is correct.

On edit: There is something about this problem that bugs me. If the frequency is 13 Hz, the period is $T = \frac{1}{13}$ s. This means that in time $t_2 = 5~s$ the number of oscillations executed is $N = t_2/T = 65$. This is an integer which means that the oscillator at $t_2$ must have the same displacement as at time $t_1 =0$.

 

[blizzardof96]

Did you check your work? Do you get a displacement of 0.04 when you put your values for A and φ back in the original equation? Your method is correct.

On edit: There is something about this problem that bugs me. If the frequency is 13 Hz, the period is $T = \frac{1}{13}$ s. This means that in time $t_2 = 5~s$ the number of oscillations executed is $N = t_2/T = 65$. This is an integer which means that the oscillator at $t_2$ must have the same displacement as at time $t_1 =0$.

I checked my work and the solution agreed with initial eqn. The values were arbitrary so its possible that they don't make physical sense.

Thank you for your help.

 

[haruspex]

6) Arctan(cos(k)-4)/sin(k))=ø

ø= -77.36 degrees

As @kuruman points out, the problem as stated is inconsistent and has no solution.
What value did you use for k?