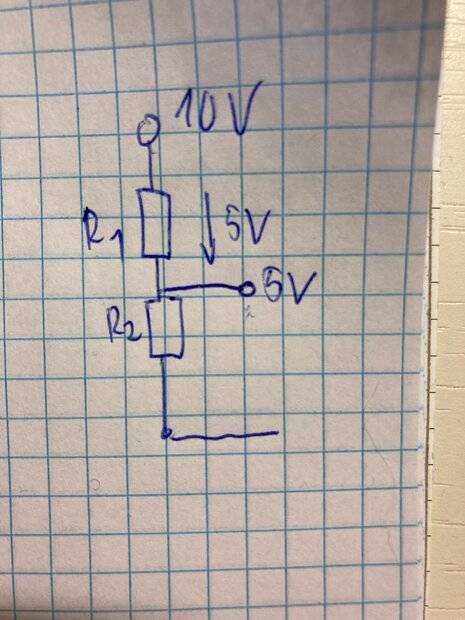Discussion Overview
The discussion revolves around the concept of voltage dividers in electrical circuits, specifically addressing how voltage can be utilized after it has been dropped across resistors. Participants explore the implications of connecting additional components to a voltage divider and the conditions under which the voltage divider formula applies.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses confusion about how to use the voltage at a node after it has been dropped across resistors, questioning if the voltage can be reused if another resistor is connected in series.
- Another participant clarifies that connecting components to the 5V point will affect the circuit, suggesting that it may be acceptable in some scenarios, such as biasing a transistor, but problematic for powering significant loads.
- A participant challenges the voltage analysis presented by another, emphasizing the need for Kirchhoff's Voltage Law (KVL) and pointing out an error in the voltage sum.
- One participant reiterates that voltage is not lost when dropped across components, but rather represents a voltage difference, and encourages checking external resources for clarification.
- Another participant agrees with the initial confusion, stating that the voltage at the node can only be maintained if no additional components are connected, and explains how adding a resistor in parallel would decrease the voltage at that node.
- A participant notes that the stability of the 5V supply depends on the resistance of the connected circuit, indicating that a high enough resistance is necessary to maintain the voltage without significant drop.
- One participant provides a corrected voltage divider calculation assuming a 12V supply, explaining the conditions under which the voltage divider formula is valid and how additional resistors affect the current and voltage distribution.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and confusion regarding the voltage divider concept. There is no consensus on the implications of connecting additional components to the voltage divider, and multiple competing views on how to apply the voltage divider formula correctly remain unresolved.
Contextual Notes
Some participants' analyses contain errors or assumptions that are not fully explored, particularly regarding the application of Kirchhoff's laws and the impact of additional resistors on voltage calculations.