crememars
- 15
- 2
- Homework Statement
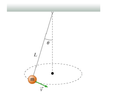
- A bob of mass m is suspended from a fixed point with a massless string of length L. You are to investigate the motion in which the string moves in a cone with half-angle, 𝜃. Express your answers in terms of some or all of the variables m, L, and 𝜃, and g.
v = √Lgsin𝜃tan𝜃
How long does it take the bob to make one full revolution (one complete trip around the circle)?
- Relevant Equations
- T = 2πr / v
r = Lsin𝜃
hi ! I'm having a lot of trouble simplifying my expression for one of my homework questions. I know someone asked about this homework problem already, but the answers didn't really help me figure out how to simplify it.. I really have no idea what steps to take, and I've even consulted all my math notes too.
my expression for T is:
T = 2πLsinθ / √(Lgsinθtanθ)
T = 2πLsinθ * √(Lgsinθtanθ) / Lgsinθtanθ
T = 2π * √(Lgsinθtanθ) / gtanθ
final answer
[ 2π * √(Lgsinθtanθ) ] / gtanθ
the correct answer should be:
2π * √( Lcosθ / g )thank you in advance
my expression for T is:
T = 2πLsinθ / √(Lgsinθtanθ)
T = 2πLsinθ * √(Lgsinθtanθ) / Lgsinθtanθ
T = 2π * √(Lgsinθtanθ) / gtanθ
final answer
[ 2π * √(Lgsinθtanθ) ] / gtanθ
the correct answer should be:
2π * √( Lcosθ / g )thank you in advance