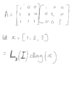Simplifying a matrix into an equation

  • Context: Undergrad 
  • Thread starter Thread starter Joes12
  • Start date Start date
  • Tags Tags
    Matrix Simplifying
Click For Summary
SUMMARY

The discussion centers on decomposing a matrix into a product of two matrices and the notation involved in this process. The user seeks to express a lower triangular matrix, denoted as L, multiplied by a diagonal matrix derived from a column vector, specifically vector x. The conversation highlights the need for padding to align matrix sizes for operations akin to the Hadamard product. The user also questions the validity of using L(J_n) to represent the lower triangular matrix with non-zero elements set to one.

PREREQUISITES
  • Matrix decomposition techniques
  • Understanding of lower triangular matrices
  • Knowledge of the Hadamard product
  • Matrix padding methods for size alignment
NEXT STEPS
  • Research matrix decomposition methods, focusing on lower triangular matrices
  • Explore the Hadamard product and its applications in matrix operations
  • Learn about padding techniques for matrices to facilitate operations
  • Investigate valid notations for matrix representations in mathematical contexts
USEFUL FOR

Mathematicians, data scientists, and anyone involved in linear algebra or matrix operations seeking to understand matrix decomposition and manipulation techniques.

Joes12
Messages
8
Reaction score
0
TL;DR
Im looking to simplify a matrix and express it in a more compact equation form if possible
Hi,

Please see the attached image. I have a matrix and would like to split it up into a nice compact equation if possible. Matrix A seems to be a nice pattern that would lend itself to writing in equation form but I’m not sure what to do. Is it possible? Also do you know how I could correctly separate the column vector out? Would I need to add some padding to this? How would you do that? Many thanks.
 

Attachments

  • 37CEAAF7-8E65-43FB-910A-97618BF9AE50.jpeg
    37CEAAF7-8E65-43FB-910A-97618BF9AE50.jpeg
    23.6 KB · Views: 218
Physics news on Phys.org
It's not clear what you are trying to do. The product of a matrix and a vector is another vector; not another matrix.

It is possible to decompose a matrix into a product of two matrices.
 
I think I’ve found a way to calculate the A part. Is my notation correct? What I am trying to say is take the lower triangular matrix of the Identity matrix, so that it results in all ones of the lower triangular part. Then multiply this by the diagonal matrix of vector x. Please see attached.

Any idea how to progress the a part? Is there something like a hadamard product operation but for a matrix and a column vector? Thanks again :)
 

Attachments

  • 985877B5-B7DD-49D8-8832-B6C5B690CA2D.jpeg
    985877B5-B7DD-49D8-8832-B6C5B690CA2D.jpeg
    14.7 KB · Views: 219
I still don't see what equality you are looking for.
 
Appologies I think I should have written J instead of I.

From what I read, the symbol for the lower triangular matrix is L. If I want the non-zero elements of L to be 1 can I write L(J_n)? Is that valid notation to describe that situation?

What I am looking to say with the a part is, take each element in the resulting matrix above and multiply each of the elements by the value given in the column vector with the same row.

eg: [1 2 ;3 4] some operation [10 20]^T = [1*10 2*10; 3*20 4*20]

The Hadamard product is kind of like what I want to do however I am looking for matrices of different sizes.

Is there a way to succinctly say, pad to make the matrices the same size, perform Hadamard product and then remove the unwanted elements?
 
I think Iv found the answer. Is it valid to write L(J_n) though? Thanks again
 

Similar threads

Undergrad Matrix rank in terms of determinant polynomial
  • · Replies 14 ·
Replies
14
Views
3K
Undergrad Index notation of vector rotation
  • · Replies 7 ·
Replies
7
Views
2K
Undergrad Solving matrix commutator equations?
  • · Replies 7 ·
Replies
7
Views
4K
Undergrad Symbol for matrix representative of a tensor
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Uniqueness of reduced row echelon form (proof verification)
  • · Replies 4 ·
Replies
4
Views
2K
High School Row reduction, Gaussian Elimination on augmented matrix
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Matrix diagonalization algorithm
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Problem with notation of matrix elements
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad What Does the F Matrix Look Like for a Linear Bezier Curve?
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Consistent matrix index notation when dealing with change of basis
  • · Replies 12 ·
Replies
12
Views
2K