washablemarker
- 12
- 0
[SOLVED] Sketching the Curves of a Function W/In an Interval - Simple (1st Year Calcu
Sketch the graph of the function on the interval [0, 2pi].
y = cosx - 1/2(cos2x)
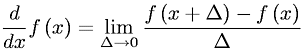
so the problems that i have been practicing like this have been pretty simple. i determine all of the following:
the problem is that mathematically i located a single extreme value at (pi, -3/2), but graphically, there appears to be more.
http://img149.imageshack.us/img149/1645/graphscreenshotth2.th.png
is not each change in direction a relative minimum/maximum value? i can only seem to locate the absolute minimum value within the interval, but none of the other relative extreme values. any idea as to where i am going wrong?
so, the first derivative of the given function is -sinx + sin2x. solving this equation is where i find possible extrema at 0, pi, and 2pi. any ideas why i can't seem to locate the other extrema algebraically?
Homework Statement
Sketch the graph of the function on the interval [0, 2pi].
y = cosx - 1/2(cos2x)
Homework Equations
The Attempt at a Solution
so the problems that i have been practicing like this have been pretty simple. i determine all of the following:
- domain and range
- x and y intercepts
- whether or not there is discontinuity
- whether or not there is symmetry
- intervals of increasing and decreasing order
- extrema
- points of inflection
- concavity
- whether or not there exist asymptotes
the problem is that mathematically i located a single extreme value at (pi, -3/2), but graphically, there appears to be more.
http://img149.imageshack.us/img149/1645/graphscreenshotth2.th.png
is not each change in direction a relative minimum/maximum value? i can only seem to locate the absolute minimum value within the interval, but none of the other relative extreme values. any idea as to where i am going wrong?
so, the first derivative of the given function is -sinx + sin2x. solving this equation is where i find possible extrema at 0, pi, and 2pi. any ideas why i can't seem to locate the other extrema algebraically?
Last edited by a moderator: