icecats
- 5
- 0
I am in a mechanical design class that has been focusing on the slider crank mechanism. My professor tends to just provide derived equations without showing the analysis. I feel like I am missing out on some key understanding because of this. Specifically, I am trying to do what should be a simple force analysis on a simplified slider crank. However, my results are not matching up with what the professors equations suggest.
In the attached pictures, Case 1 shows the slider crank in one position and Case 2 shows it in a different position. Based on a statics force analysis, I would expect that, for the same torque T, the equilibrium force F in Case 1 would be higher than Case 2. In fact, I would expect that F in Case 2 would be 0. However, the equations provided in class and intuition from the operation of a slider crank suggest the opposite. What am I doing wrong? I feel like it has something to do with the fact that the joints are pin joints and not rigid.
Thanks!

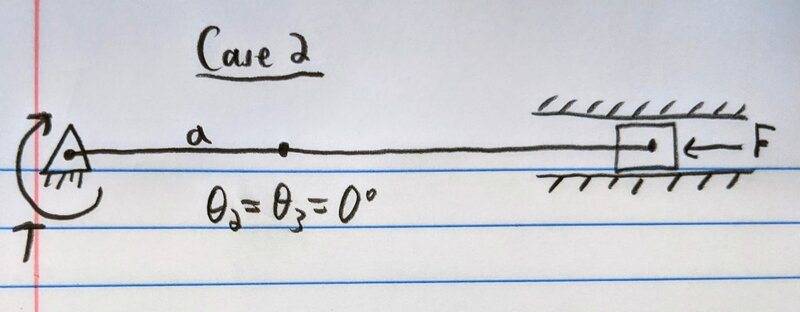
In the attached pictures, Case 1 shows the slider crank in one position and Case 2 shows it in a different position. Based on a statics force analysis, I would expect that, for the same torque T, the equilibrium force F in Case 1 would be higher than Case 2. In fact, I would expect that F in Case 2 would be 0. However, the equations provided in class and intuition from the operation of a slider crank suggest the opposite. What am I doing wrong? I feel like it has something to do with the fact that the joints are pin joints and not rigid.
Thanks!