MatinSAR
- 673
- 204
- Homework Statement
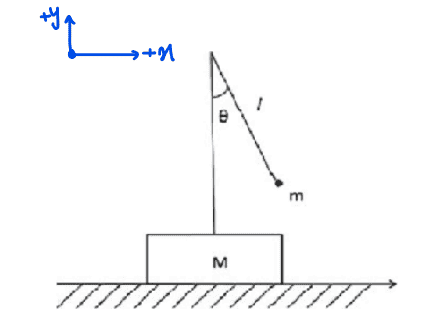
- A simple pendulum with mass ##m## and length ##L## is placed on a block with mass ##M##. The block can move freely on a frictionless horizontal surface. Find the equation of motion and the frequency of small oscillations.
- Relevant Equations
- Hamilton's principle and Lagrangian equation.
Hello. This is the figure of the problem:
First, we should determine the Lagrangian of the system. I have already completed this part without any issues. To respect everyone’s time, I won’t go into the details of how I accomplished it.
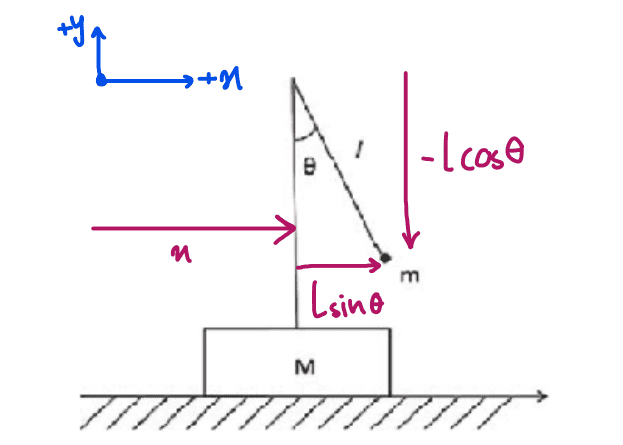
$$L=\dfrac {M+m}{2}\dot x^2+ml\dot x \dot \theta \cos \theta + \dfrac 1 2 m l^2 \dot \theta^2 +mgl\cos \theta $$ To find equation of motion I should directly put the above lagrangian in lagrange's equation? Or is it possible to first simplify it for small oscillations?
Edit 1: I forgot to mention that for small oscillations we can ignore the higher powers of theta and its derivatives.
First, we should determine the Lagrangian of the system. I have already completed this part without any issues. To respect everyone’s time, I won’t go into the details of how I accomplished it.
$$L=\dfrac {M+m}{2}\dot x^2+ml\dot x \dot \theta \cos \theta + \dfrac 1 2 m l^2 \dot \theta^2 +mgl\cos \theta $$ To find equation of motion I should directly put the above lagrangian in lagrange's equation? Or is it possible to first simplify it for small oscillations?
Edit 1: I forgot to mention that for small oscillations we can ignore the higher powers of theta and its derivatives.
Last edited: