Homework Help Overview
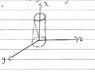
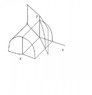
The problem involves evaluating a triple integral of the form ∫ ∫ ∫ zDv over a solid G, which is defined by the cylinder (y^2) + (z^2) = 1 and is cut by the planes y = x, x = 0, and z = 0. Participants are exploring the geometric interpretation of the solid and its boundaries.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
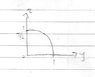
- Participants discuss the shape and boundaries of the solid, questioning how the planes intersect with the cylinder and the implications for the solid's volume. There are inquiries about the limits of integration and the use of cylindrical coordinates.
Discussion Status
The discussion is ongoing, with participants providing insights into the geometric configuration of the solid. Some have attempted to visualize the solid and clarify the role of the bounding planes, while others are questioning the appropriateness of their coordinate system and integral setup.
Contextual Notes
There are mentions of confusion regarding the projection of the solid onto different planes and the implications for using cylindrical coordinates. Participants are also addressing the constraints imposed by the first octant and the nature of the solid's base.