- #1
dislect
- 166
- 0
hi all 
i apologize in advance for the poor englsih, the question is translated from another language.
A round beam (radius R) is harnessed on the left side to a wall.
The beam is made up of two parts glued together by a thin layer of glue - the attachment plane is described in the picture as AB.
A 'glue fail' happens when the SIZE of the shear strain on plane AB is bigger the Sigma0 (some unkown value).
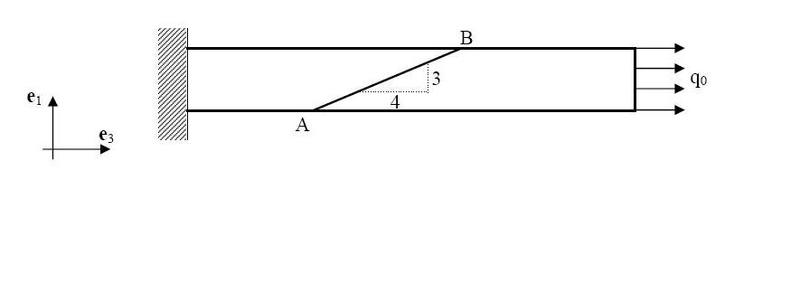
On the right side of the beam there's an equaly spred strain q=q0*e3 (note that q0 might be negetive as well).
What is the allowed value range of q0 so that there won't be a glue failure? (express your answer by using R and Sigma0)
this question was given as a challenge, and is a part of a course called solid mechanics 2 that deals more with shear strain and strain matrices. I really don't even have a clue of how to begin, i can't see how the radius R plays a part in the answer..
help, please?
i apologize in advance for the poor englsih, the question is translated from another language.
A round beam (radius R) is harnessed on the left side to a wall.
The beam is made up of two parts glued together by a thin layer of glue - the attachment plane is described in the picture as AB.
A 'glue fail' happens when the SIZE of the shear strain on plane AB is bigger the Sigma0 (some unkown value).
On the right side of the beam there's an equaly spred strain q=q0*e3 (note that q0 might be negetive as well).
What is the allowed value range of q0 so that there won't be a glue failure? (express your answer by using R and Sigma0)
this question was given as a challenge, and is a part of a course called solid mechanics 2 that deals more with shear strain and strain matrices. I really don't even have a clue of how to begin, i can't see how the radius R plays a part in the answer..
help, please?