vibha_ganji
- 19
- 6
This is the problem statement from the textbook.
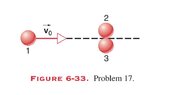
“A ball with an initial speed of 10.0 m/s collides elastically with two identical balls whose centers are on a line perpendicular to the initial velocity and that are initally in contact with each other (Fig. 6-33). The first ball is aimed directly at the contact point and all the balls are frictionless. Find the velocities of all three balls after the collision. (Hint: With friction absent, each impulse is directed along the line of centers of the balls, normal to the colliding surfaces.)”
The solution in the Instructor’s Manual states the following, “
All three balls are identical in mass and radii? Then balls 2 and 3 will move off at 30 ◦ to the initial direction of the first ball. By symmetry we expect balls 2 and 3 to have the same speed. The problem now is to define an elastic three body collision. It is no longer the case that the balls bounce off with the same speed in the center of mass. One can’t even treat the problem as two separate collisions, one right after the other. No amount of momentum conservation laws will help solve the problem; we need some additional physics, but at this point in the text we don’t have it.”
I am unable to understand how they concluded that the balls move off at 30 degrees to the initials direction of the first ball. I tried using the conservation of momentum but was unable to reach this conclusion.
“A ball with an initial speed of 10.0 m/s collides elastically with two identical balls whose centers are on a line perpendicular to the initial velocity and that are initally in contact with each other (Fig. 6-33). The first ball is aimed directly at the contact point and all the balls are frictionless. Find the velocities of all three balls after the collision. (Hint: With friction absent, each impulse is directed along the line of centers of the balls, normal to the colliding surfaces.)”
The solution in the Instructor’s Manual states the following, “
All three balls are identical in mass and radii? Then balls 2 and 3 will move off at 30 ◦ to the initial direction of the first ball. By symmetry we expect balls 2 and 3 to have the same speed. The problem now is to define an elastic three body collision. It is no longer the case that the balls bounce off with the same speed in the center of mass. One can’t even treat the problem as two separate collisions, one right after the other. No amount of momentum conservation laws will help solve the problem; we need some additional physics, but at this point in the text we don’t have it.”
I am unable to understand how they concluded that the balls move off at 30 degrees to the initials direction of the first ball. I tried using the conservation of momentum but was unable to reach this conclusion.