Saurabh
- 9
- 0
<Moderator's note: Moved from a technical forum and thus no template.>
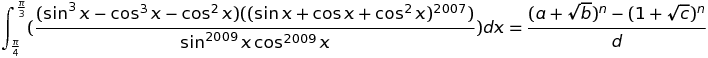
where a, b, c, d and n, all are positive integers.
Find the value of 'c'.
-------------------------------
I don't really have a good approach for this one.
I just made a substitution u = sinx + cosx
I couldn't clear up the mess.
A hint(s) would be highly appreciated.
Peace!
where a, b, c, d and n, all are positive integers.
Find the value of 'c'.
-------------------------------
I don't really have a good approach for this one.
I just made a substitution u = sinx + cosx
I couldn't clear up the mess.
A hint(s) would be highly appreciated.
Peace!
Attachments
Last edited by a moderator: