Solving 210 V Homework Equations with Multiple Loops

[gaillard]

Homework Statement

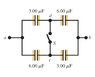
Well the only thing the problem gives is 210 V

Homework Equations

Q=VC
series Q=Q=Q..
V+V=V
1/C=1/C+1/C..
parallel
Q+Q+Q..
V=V=V..
C+C+C..

around a loop the voltage is zero.

The Attempt at a Solution

Now I have no where to begin. I can see three loops, but don't they conflict with each other? How can you go from a to b on the top, and have the charges equal to each other and then go from a to d to c to b and have those charges equal while both paths equal 210V? that would be something crazy like 4x=6x kind of thing. I don't understand what I am missing. I fine when I can combine capacitors. But I am using the young and freedman book and NO WHERE was there a problem that had capacitors you couldn't combine except the challenge problems where they didn't explain. hm.

Thanks for the help guys.

 

[Integral]

If you were to actually state the problem it would make helping you a lot easier.

 

[gaillard]

woops sorry, it asks first for the voltage between c and d when the switch is open, which I got. 70V. Then it goes to ask the potential across each capacitor when the switch is closed, which is the part I am confused about. Lastly it asks the total charge through the switch.

Thanks and sorry about that

 

[gaillard]

Ok well I got the voltages across each capacitor, but I am now stuck on how much charge flows through that switch. Shouldn't it be 210*Capacitance equivalent?

I got for 210*Ceq as 1.89*10^-3 but its wrong.

Any hints?

 

[berkeman]

How did you get the initial voltage Vcd = 70V? Where did that come from? Any chance you could copy the problem statement word-for-word, and mention any other connections that are being made to the circuit that you posted?

 

[gaillard]

The capacitors in the figure View Figure are initially uncharged and are connected, as in the diagram, with switch S open. The applied potential difference is V_{ab}= + 210 {V}.

What is the potential difference V_{cd}?
70 V
Correct
my answers

Part B
What is the potential difference V_{ad} after switch S is closed?
105 V
Correct
my answers

Part C
What is the potential difference V_{db} after switch S is closed?
105 V
Correct
my answers

Part D
What is the potential difference V_{ac} after switch S is closed?
105 V
Correct
my answers

Part E
What is the potential difference V_{cb} after switch S is closed?
105 V
Correct
my answers

Part F
How much charge flowed through the switch when it was closed?Thats everything and I am stuck on F.

70 came from the fact that when the switch is open the top capacitors are in series thus the voltages add up. 140 +70 =210 but if you look at the voltage over the first capacitor you see its 140 and the first on the bottom is 70, so subtract them and you get the voltage between c and d.

But I am really stuck on the last part.

I combines the capacitors down to one capacitor with a voltage of 210 (obviously) and a capacitance of 4.5*10^-6 F. charge equivalent being 9.45*10^-4. But that is not the correct answer...

 

[berkeman]

I would try it this way. Write the amount of charge on each capacitor before the switch is closed, and then for after the switch is closed. Charge in that middle section of the capacitor circuit will have to be conserved (no where for it to go), so see if you can figure out how much charge flowed through the switch and in which direction, in order to go from the first charge distribution to the final charge distribution.