- #31
thomas91
- 23
- 0
Orodruin said:
Sorry but... If I know
Solving a Cycloid Equation: Finding θ(t)
- Thread starter thomas91
- Start date
Click For Summary
SUMMARY
The discussion focuses on solving a cycloid equation for a bead sliding on a frictionless wire, represented by the equations x = a(θ - sin θ) and y = a(1 + cos θ) for θ in the range of 0 to 2π. Participants assist in transforming the variable using u = cos(θ/2) to derive a linear equation for u(t) and subsequently find θ(t) under initial conditions. The final solution for the oscillation period is established as T = 4π√(a/g), confirming the relationship between the parameters involved.
PREREQUISITES- Understanding of differential equations and their solutions
- Familiarity with cycloid geometry and its equations
- Knowledge of variable substitution techniques in calculus
- Basic physics concepts, particularly those related to motion and oscillation
- Study the derivation of solutions for second-order differential equations
- Learn about the properties of cycloids and their applications in physics
- Explore variable substitution methods in calculus for solving complex equations
- Investigate the principles of oscillation and period calculation in mechanical systems
Students of physics and mathematics, particularly those studying mechanics, differential equations, and oscillatory motion, will benefit from this discussion.
Sorry but... If I know
- #32
- 22,820
- 14,860
You still need to solve for ##\theta(t)##. Your solution was for \cos(\theta)##...
- #33
thomas91
- 23
- 0
Orodruin said:
Then...
Is correct? Thanks!
- #34
- 22,820
- 14,860
No, theta is a function of time.
- #35
thomas91
- 23
- 0
Then... Recapitulating
2nd condition = > θ' = 0 and t = 0 (rest position)
So I obtained B setting θ' (t = 0) = 0; so B = 0
And now, knowing A and B I have the solution for cos(θ/2)
2nd condition = > θ' = 0 and t = 0 (rest position)
So I obtained B setting θ' (t = 0) = 0; so B = 0
And now, knowing A and B I have the solution for cos(θ/2)
- #36
- 22,820
- 14,860
So theta becomes ...?thomas91 said:
- #37
thomas91
- 23
- 0
Hello!
¿
?
Thanks!
¿
Thanks!
- #38
- 22,820
- 14,860
There we go!thomas91 said:Hello!
¿?
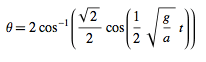
Thanks!
- #39
thomas91
- 23
- 0
Finally! How can I calculate the oscillation period of the bean?
- #40
- 22,820
- 14,860
How long does it take until it returns to the original position?
- #41
thomas91
- 23
- 0
It will be
?
Simplified:
Thanks!
Simplified:
Thanks!
- #42
- 22,820
- 14,860
Bingo!
Or even simpler
$$
T= 4\pi \sqrt{\frac{a}{g}}
$$
Or even simpler
$$
T= 4\pi \sqrt{\frac{a}{g}}
$$
- #43
thomas91
- 23
- 0
Thanks for everything Orodruin! Have a nice day :D
Similar threads
- · Replies 29 ·
- · Replies 26 ·
- · Replies 3 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 4 ·
- · Replies 4 ·
- · Replies 2 ·