pyroknife
- 611
- 4
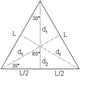
This is from a electric field problem I'm trying to solve. This part I'm asking is geometry. I'm trying to find the distance from a corner of a equilateral triangle to its center. Also, I have to find the distance from the midpoint of a baseline to the center of the triangle.
Let's assume each side length is 2. Let's also assume that a corner lies at the top and the 2 other corners lie at the bottom like this pic http://upload.wikimedia.org/wikipedi...quilateral.svg . So I divide the triangle in half to find its height through the pythagorean theorem. 2^2-(2/2)^2=3. sqrt(3)=height. Then I divided the height by 2 and got .866 (using decimals cause idk how to type a square root symbol.) So wouldn't the .866 be the distance from the center to the midpoint of the baseline? Also, wouldn't it make it the distance from the top corner of the triangle to the center?? If that's the case doesn't that contradict the belief that all 3 corners have the same distance to the center of a equilateral triangle.
But when you calculate the distance from the corner to the center. You use the pythagorean thereom again. You have 1 for the base length and .866 for the height right? That gives you a hypotenuse of sqrt(1.75) which doesn't equal .866?
Can someone explain this to me please.
Let's assume each side length is 2. Let's also assume that a corner lies at the top and the 2 other corners lie at the bottom like this pic http://upload.wikimedia.org/wikipedi...quilateral.svg . So I divide the triangle in half to find its height through the pythagorean theorem. 2^2-(2/2)^2=3. sqrt(3)=height. Then I divided the height by 2 and got .866 (using decimals cause idk how to type a square root symbol.) So wouldn't the .866 be the distance from the center to the midpoint of the baseline? Also, wouldn't it make it the distance from the top corner of the triangle to the center?? If that's the case doesn't that contradict the belief that all 3 corners have the same distance to the center of a equilateral triangle.
But when you calculate the distance from the corner to the center. You use the pythagorean thereom again. You have 1 for the base length and .866 for the height right? That gives you a hypotenuse of sqrt(1.75) which doesn't equal .866?
Can someone explain this to me please.
Last edited by a moderator: